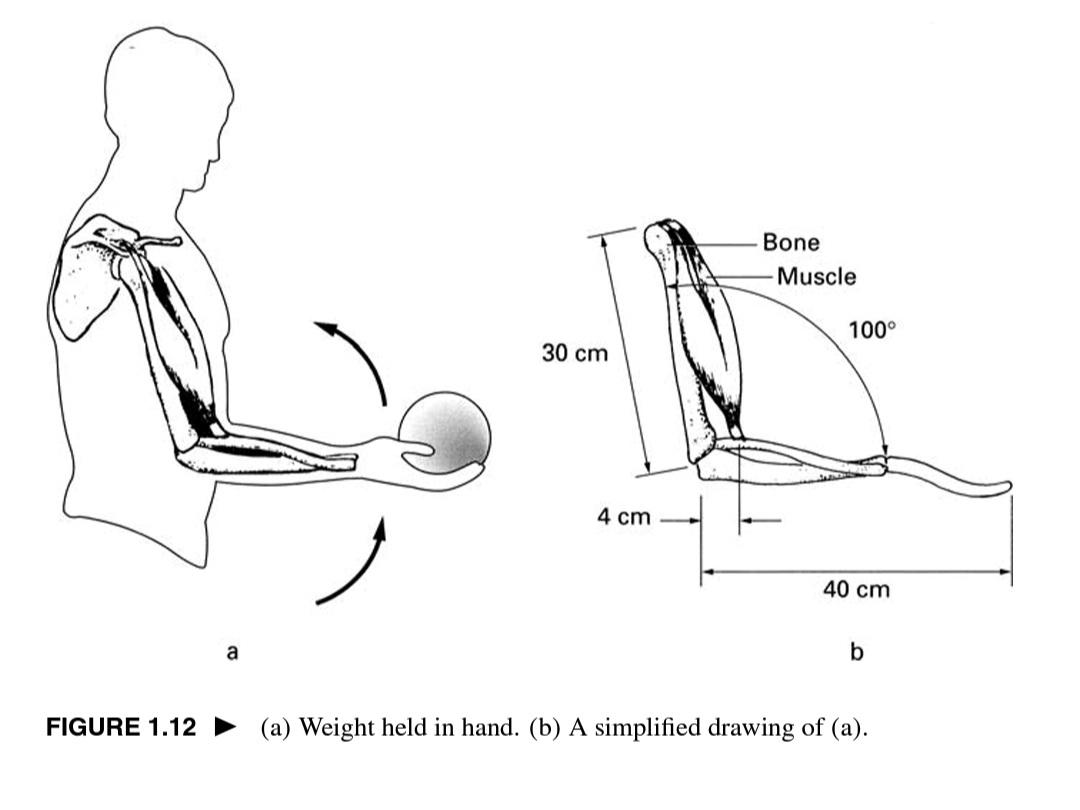
3. Using trigonometry, calculate the angle 0 in Fig. 1.13. The dimensions are specified in Fig. 1.12b. 4. Using the data provided in the text, calculate the maximum weight that the arm can support in the position shown in Fig. 1.12. Bone Muscle 100 30 cm 4 cm 40 cm a FIGURE 1.12 (a) Weight held in hand. (b) A simplified drawing of (a). 100 angle. A simplified diagram of this arm position is shown in Fig. 1.12b. The dimensions shown in Fig. 1.12 are reasonable for a human arm, but they will, of course, vary from person to person. The weight pulls the arm down- ward. Therefore, the muscle force acting on the lower arm must be in the up direction. Accordingly, the prime active muscle is the biceps. The position of the upper arm is fixed at the shoulder by the action of the shoulder muscles. We will calculate, under the conditions of equilibrium, the pulling force Fm exerted by the biceps muscle and the direction and magnitude of the reaction force F, at the fulcrum (the joint). The calculations will be performed by con- sidering the arm position as a Class 3 lever, as shown in Fig. 1.13. The x- and y-axes are as shown in Fig. 1.13. The direction of the reaction force F, shown is a guess. The exact answer will be provided by the calculations. In this problem we have three unknown quantities: the muscle force Fm, 32 the reaction force at the fulcrum Fr, and the angle, or direction, of this force p. The angle 0 of the muscle force can be calculated from trigonometric con- siderations, without recourse to the conditions of equilibrium. As is shown in Exercise 1-3, the angle 0 is 72.6. For equilibrium, the sum of the x and y components of the forces must each be zero. From these conditions we obtain Fm cos 0 = F, cos o (1.10) (1.11) x components of the forces: y components of the forces: Fm sin e = W+ F, sin o These two equations alone are not sufficient to determine the three unknown quantities. The additional necessary equation is obtained from the torque con- ditions for equilibrium. In equilibrium, the torque about any point in Fig. 1.13 must be zero. For convenience, we will choose the fulcrum as the point for our torque balance. 14 Chapter 1 Static Forces The torque about the fulcrum must be zero. There are two torques about this point: a clockwise torque due to the weight and a counterclockwise torque due to the vertical y component of the muscle force. Since the reaction force Fr acts at the fulcrum, it does not produce a torque about this point. Using the dimensions shown in Fig. 1.12, we obtain 4 cm x Fm sin 0 = 40 cm x W or Fm sin e = 1OW (1.12) Therefore, with 0 = 72.6, the muscle force Fm is 10 W Fm = 10.5 W (1.13) 0.954 With a 14-kg (31-lb) weight in hand, the force exerted by the muscle is Fm = 10.5 x 14 x 9.8 = 1440 N (325 lb) If we assume that the diameter of the biceps is 8 cm and that the muscle can produce a 7 x 10 dyn force for each square centimeter of area, the arm is capable of supporting a maximum of 334 N (75 lb) in the position shown in Fig. 1.13 (see Exercise 1-4). The solutions of Eqs. 1.10 and 1.11 provide the magnitude and direction of the reaction force Fr. Assuming as before that the weight supported i 14 kg, these equations become 1440 x cos 72.6 = F, cos o 1440 x sin 72.6 = 14 x 9.8+ F, sin (1. or II