Question: Number 2 please! Couldn't crop smaller 1. Let G be a group. Prove that if a E G is the only element of order 2

Number 2 please! Couldn't crop smaller

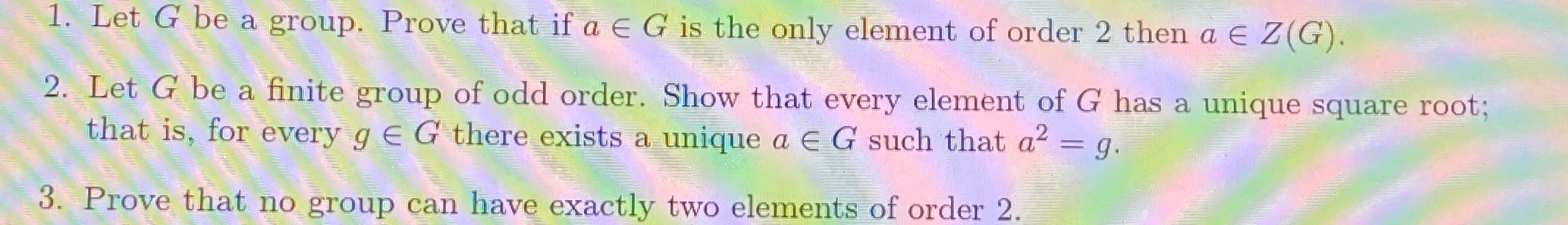
1. Let G be a group. Prove that if a E G is the only element of order 2 then a E Z (G). 2. Let G be a finite group of odd order. Show that every element of G has a unique square root; that is, for every g E G there exists a unique a E G such that a2 = g. 3. Prove that no group can have exactly two elements of order 2

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

1. One measure used to assess competitive advantage is shareholder value creation. How would you assess PepsiCos performance? 2. If you were to apply a triple-bottom-line approach to assessing...

I need help on those questions please! 1. Let G be a group such that every element in G has order 2, i.e. for all g E G, 92 = 69. Prove that G is an abelian group. Recall, G is an abelian group if ab...

Explain it l. 2. 12. 13. 14. 15. Show that a group having five or less elements is abelian. For elements a, b, x in a group G. Show that (0 0(a) = 0(0") (a) 0(a) = o(x\"lax). (iii) 0(0") 5 0(a) (iv)...

I need help on those 5 response question in bullet point in the last screenshot out of 7 below please! 1 Cosets and Lagrange 1. Let G be a group of order 60. What are the possible orders for the...

1. Suppose that a is a group element and a" = e. What are the possibilities for la |? Provide justification for your answer. 2. Consider the set {4,8,12,16}. Show that this set is a group under...

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

Explain ments of nite order does it have? 20. Suppose that G is an Abelian group of order 35 and every element of G satises the equation x35 = e. Prove that G is cyclic. Does your argument work if 35...

18. 19. 20. 21. 22. 23. 24. 25 26 27 29. 30. 31. 32. 33. 34. 35. Suppose that a is a group element and a6 E e. What are the possi- bilities for lal? Provide reasons for your answer. If a is a group...

Please solve step by step and Do not Use chatGPT or AI tools I know answers are available in chegg but those are perfectly wrong. Please solve if know the concept.. Number Theory Topics covered:...

in those partice question could you help me to fix my mistake here is my work since Ais has element of ( mhumn ) order by counter example Lom ( 7. 5. 1 )= 35 2 ? so Ais has no element of order 42 do...

19. 20. 21. 22. 23. 24. 25. 26. 27 29. 30. 31. 32. 33. 34. 35. d If a is a group element and a has innite order, prove that a'" as a" when m a n. For any group elements a and b, prove that lab! =...

Which of the following statements concerning pro forma disclosures is not true? a) They show the effects of major transactions that occur after the end of the fiscal period. b) They show the effects...

During a DVD presentation, vice presidents of marketing and sales of IBM emphasized the growing importance of team selling in their company. what are the reasons they gave for this emphasis on team...

This year Allison drove 8 0 0 miles to volunteer in a project sponsored by a qualified charitable organization in Utah. In addition, she spent $ 2 5 0 for meals while away from home. In total,...

A company is preparing completing their Cash Budget. The following data has been prepared for cash receipts and payments. January February March Cash receipts $1,061,200 $1,182,400 $1,091,700 Cash...