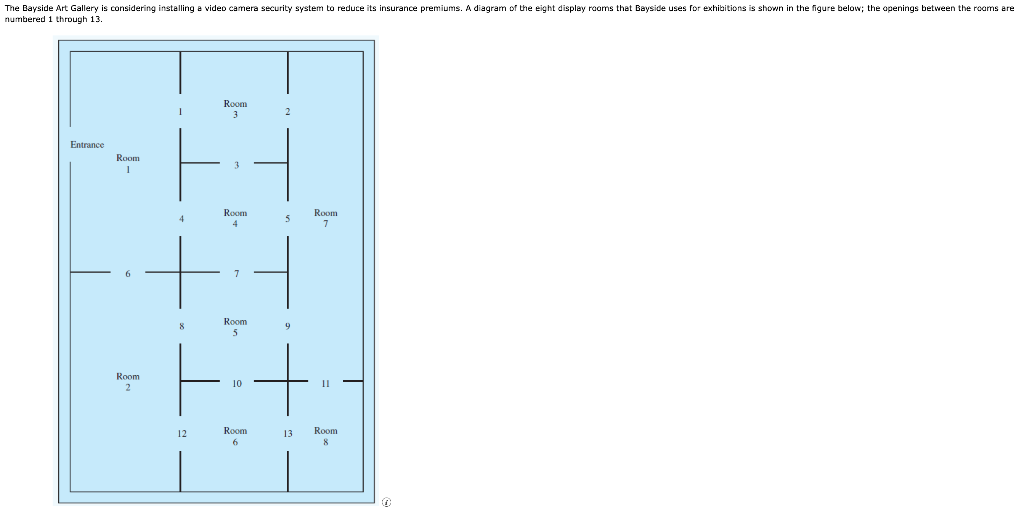
numbered 1 through 13 . (c) A security firm proposed that two-way cameras be installed at some room openings. Each camera has the ability to monitor the two rooms between which the camera is located. For example, if a camera were located at opening number 4 , rooms 1 and 4 would be covered; if a camera were located at opening 11 , rooms 7 and 8 would be covered; and so on. Management decided not to locate a camera system at the entrance to the display rooms. The objective is to provide security coverage for all eight rooms using the minimum number of two-way cameras. (a) Formulate a 0-1 integer linear programming model that will enable Bayside's management to determine the locations for the camera systems. (Let xj be the 01 which is 1 if a camera is installed at opening i, and 0 otherwise, for i=1,2,, 13.) Min s.t. Room 1 Room 2 Room 3 Room 4 Room 5 Room 6 Room 7 Room 8 xi=0,1, for i=1,2,,13 (b) Solve the model formulated in part (a) to determine how many two-way cameras to purchase and where they should be located. The gallery should install cameras with (x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13)=( (c) Suppose that management wants to provide additional security coverage for room 7 . Specifically, management wants room 7 to be covered by two cameras. Which constraint would have to change? Room 1 Room 2 Room 3 Room 4 Room 5 Room 6 Room 7 Room 8 What should the new constraint be? (d) With the policy restriction specified in part (c), determine how many two-way camera systems will need to be purchased and where they will be located. The gallery should install cameraswith(x1,x2,x3,x4,x5,x6,x7,x8x9,x10,x11,x12,x13)=(). numbered 1 through 13 . (c) A security firm proposed that two-way cameras be installed at some room openings. Each camera has the ability to monitor the two rooms between which the camera is located. For example, if a camera were located at opening number 4 , rooms 1 and 4 would be covered; if a camera were located at opening 11 , rooms 7 and 8 would be covered; and so on. Management decided not to locate a camera system at the entrance to the display rooms. The objective is to provide security coverage for all eight rooms using the minimum number of two-way cameras. (a) Formulate a 0-1 integer linear programming model that will enable Bayside's management to determine the locations for the camera systems. (Let xj be the 01 which is 1 if a camera is installed at opening i, and 0 otherwise, for i=1,2,, 13.) Min s.t. Room 1 Room 2 Room 3 Room 4 Room 5 Room 6 Room 7 Room 8 xi=0,1, for i=1,2,,13 (b) Solve the model formulated in part (a) to determine how many two-way cameras to purchase and where they should be located. The gallery should install cameras with (x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13)=( (c) Suppose that management wants to provide additional security coverage for room 7 . Specifically, management wants room 7 to be covered by two cameras. Which constraint would have to change? Room 1 Room 2 Room 3 Room 4 Room 5 Room 6 Room 7 Room 8 What should the new constraint be? (d) With the policy restriction specified in part (c), determine how many two-way camera systems will need to be purchased and where they will be located. The gallery should install cameraswith(x1,x2,x3,x4,x5,x6,x7,x8x9,x10,x11,x12,x13)=().