Numerical Analysis Question

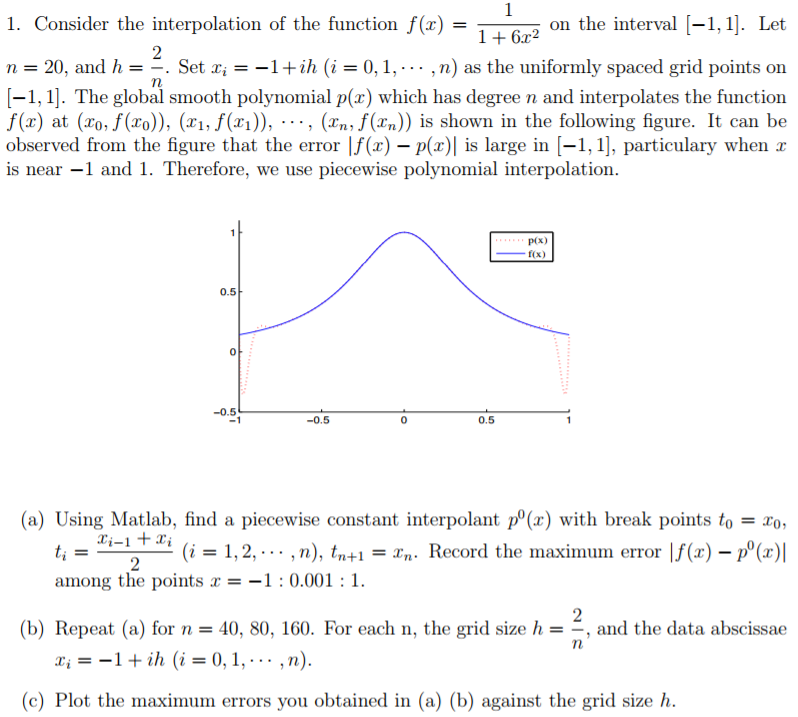
1. Consider the interpolation of the function f(x) -on the interval [-1,1]. Let 1 + 6x2 n 20, and hSet 1ih (i0,1,... ,n) as the uniformly spaced grid points on 1-1, 11. The global smooth polynomial p(x) which has degree n and interpolates the function f(x) at (xo, f(xo)), (x, f(xi)), -., (xn, f(zn)) is shown in the following figure. It can be observed from the figure that the error |f(x) - p() is large in [-1,1], particulary when r is near -1 and 1. Therefore, we use piecewise polynomial interpolation P(x) 0.5 0 -0.5 -0.5 0 0.5 (a) Using Matlab, find a piecewise constant interpolant p( with break points to o (i-1,2,... ,n), tnti- Record the maximum error f(x) -p() among the points r--1: 0.001 : 1. (b) Repeat (a) for n 40, 80, 160. For each n, the grid size h--, and the data abscissae (c) Plot the maximum errors you obtained in (a) (b) against the grid size h 1. Consider the interpolation of the function f(x) -on the interval [-1,1]. Let 1 + 6x2 n 20, and hSet 1ih (i0,1,... ,n) as the uniformly spaced grid points on 1-1, 11. The global smooth polynomial p(x) which has degree n and interpolates the function f(x) at (xo, f(xo)), (x, f(xi)), -., (xn, f(zn)) is shown in the following figure. It can be observed from the figure that the error |f(x) - p() is large in [-1,1], particulary when r is near -1 and 1. Therefore, we use piecewise polynomial interpolation P(x) 0.5 0 -0.5 -0.5 0 0.5 (a) Using Matlab, find a piecewise constant interpolant p( with break points to o (i-1,2,... ,n), tnti- Record the maximum error f(x) -p() among the points r--1: 0.001 : 1. (b) Repeat (a) for n 40, 80, 160. For each n, the grid size h--, and the data abscissae (c) Plot the maximum errors you obtained in (a) (b) against the grid size h