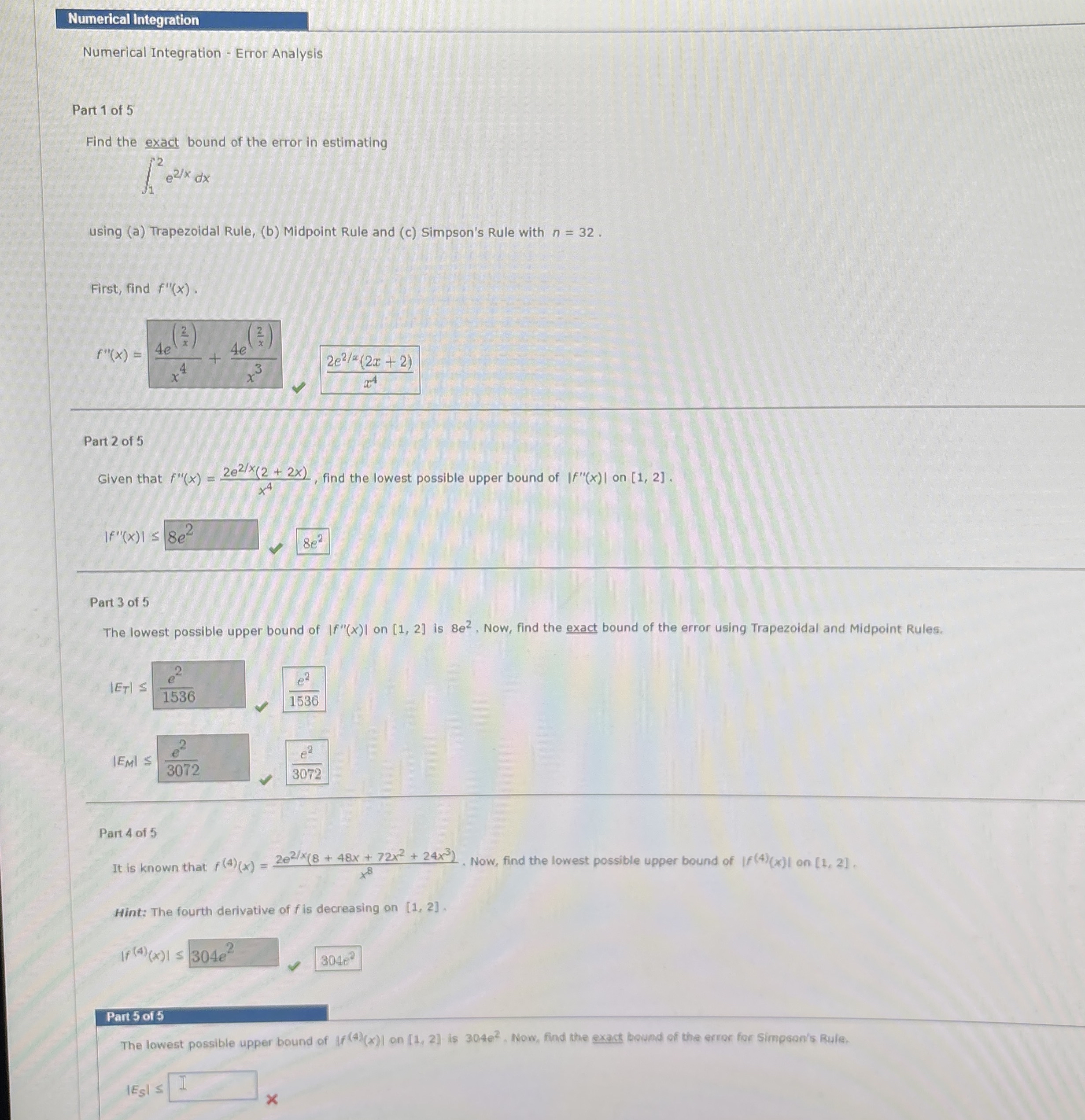
Numerical Integration

Numerical Integration $-$ Error Analysis

Part $1$ of $5$

Find the exact bound of the error in estimating

${\displaystyle \underset{1}{\overset{2}{}}}{e}^{\frac{2}{x}}dx$

using $($a$)$ Trapezoidal Rule, $($b$)$ Midpoint Rule and $($c$)$ Simpson's Rule with $n=32.$

First, find $f^{\text{'}\text{'}}(x).$

$f^{\text{'}\text{'}}(x)=\frac{4e^{(\frac{2}{x})}}{x^4}\frac{4e^{(\frac{2}{x})}}{x^3}$

Part $2$ of $5$

Given that $f^{\text{'}\text{'}}(x)=\frac{2e^{\frac{2}{x}}(22x)}{x^4},$ find the lowest possible upper bound of $|f^{\text{'}\text{'}}(x)|$ on $1,2.$

$|f^{\text{'}\text{'}}(x)|,8e^2$

Part $3$ of $5$

The lowest possible upper bound of $|f^{\text{'}\text{'}}(x)|$ on $1,2$ is $8e^2,$ Now, find the exact bound of the error using Trapezoidal and Midpoint Rules.

$|E_M|\frac{e^2}{3072},\frac{e^2}{3072}$

Part $4$ of $5$

It is known that $f^{(4)}(x)=\frac{2e^{\frac{2}{x}}(848x72x^{2}24x^3)}{x^8}.$ Now, find the lowest possible upper bound of $|f(4)(x)|$ on $1,2.$

Hint: The fourth derivative of $f$ is decreasing on $1,2.$

$|f^{(4)}(x)|304e^2$

Part $5$ of $5$

The lowest possible upper bound of $|f^{(4)}(x)|$ on $1,2$ is $304e^2.$ Now, find the exact bound of the error for simpson's Rule. $|E_s|$