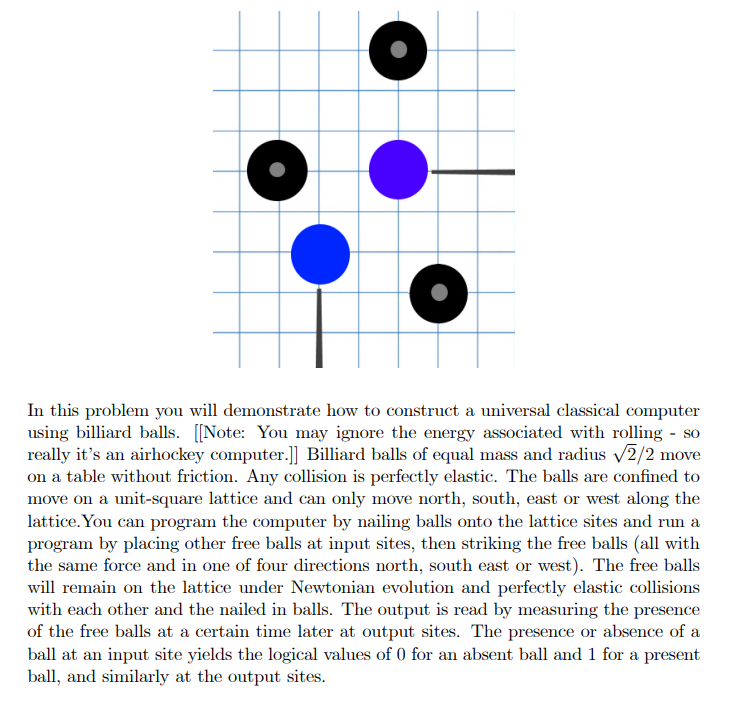
O In this problem you will demonstrate how to construct a universal classical computer using billiard balls. [[Note: You may ignore the energy associated with rolling - so really it's an airhockey computer.]] Billiard balls of equal mass and radius V2/2 move on a table without friction. Any collision is perfectly elastic. The balls are confined to move on a unit-square lattice and can only move north, south, east or west along the lattice. You can program the computer by nailing balls onto the lattice sites and run a program by placing other free balls at input sites, then striking the free balls (all with the same force and in one of four directions north, south east or west). The free balls will remain on the lattice under Newtonian evolution and perfectly elastic collisions with each other and the nailed in balls. The output is read by measuring the presence of the free balls at a certain time later at output sites. The presence or absence of a ball at an input site yields the logical values of 0 for an absent ball and 1 for a present ball, and similarly at the output sites. (a) First, a digression. Consider the switch gate: X Note that in the diagram, means "NOT 2." This gate maps {0,1}? {0,1}} so is clearly not reversible. However, it can be made reversible by restricting the allowed output set to a reversible subset. What is this subset? (b) Show that the switch gate is universal by demonstrating that you can create AND, NOT and COPY gates from it. (c) Build a switch gate using a billiard ball computer. You will need to choose two input sites representing r and y and three output sites representing z', y', and '. You will need to use two balls that are nailed in to program the computer. Your answer should be a sketch of the billiard table including the grid and the possible paths that the free balls follow during the running of the program. O In this problem you will demonstrate how to construct a universal classical computer using billiard balls. [[Note: You may ignore the energy associated with rolling - so really it's an airhockey computer.]] Billiard balls of equal mass and radius V2/2 move on a table without friction. Any collision is perfectly elastic. The balls are confined to move on a unit-square lattice and can only move north, south, east or west along the lattice. You can program the computer by nailing balls onto the lattice sites and run a program by placing other free balls at input sites, then striking the free balls (all with the same force and in one of four directions north, south east or west). The free balls will remain on the lattice under Newtonian evolution and perfectly elastic collisions with each other and the nailed in balls. The output is read by measuring the presence of the free balls at a certain time later at output sites. The presence or absence of a ball at an input site yields the logical values of 0 for an absent ball and 1 for a present ball, and similarly at the output sites. (a) First, a digression. Consider the switch gate: X Note that in the diagram, means "NOT 2." This gate maps {0,1}? {0,1}} so is clearly not reversible. However, it can be made reversible by restricting the allowed output set to a reversible subset. What is this subset? (b) Show that the switch gate is universal by demonstrating that you can create AND, NOT and COPY gates from it. (c) Build a switch gate using a billiard ball computer. You will need to choose two input sites representing r and y and three output sites representing z', y', and '. You will need to use two balls that are nailed in to program the computer. Your answer should be a sketch of the billiard table including the grid and the possible paths that the free balls follow during the running of the program