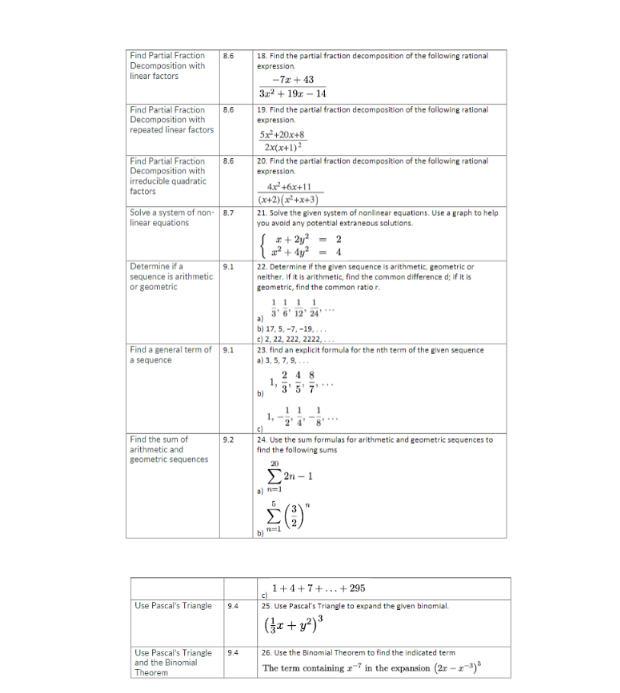
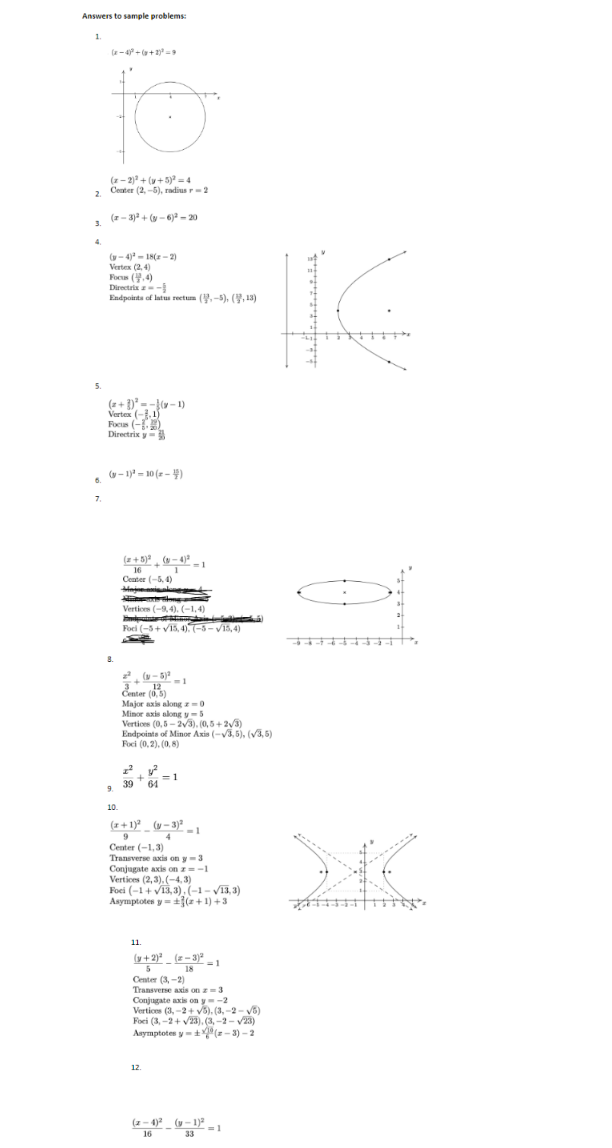
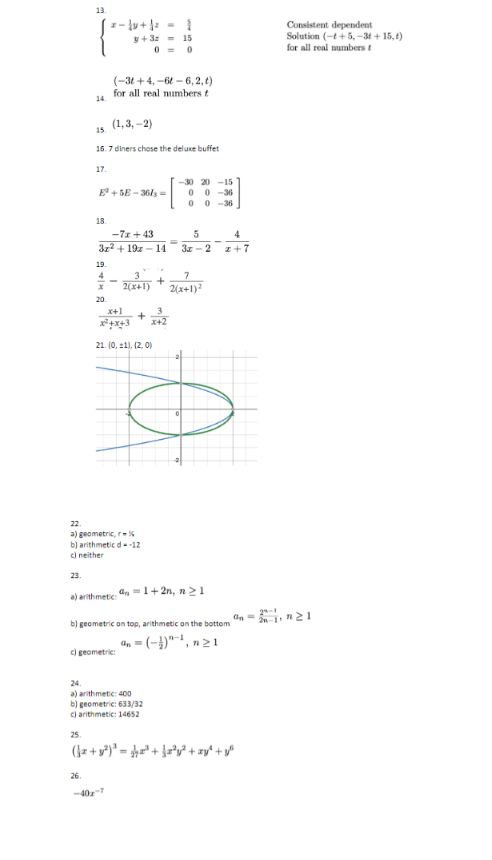
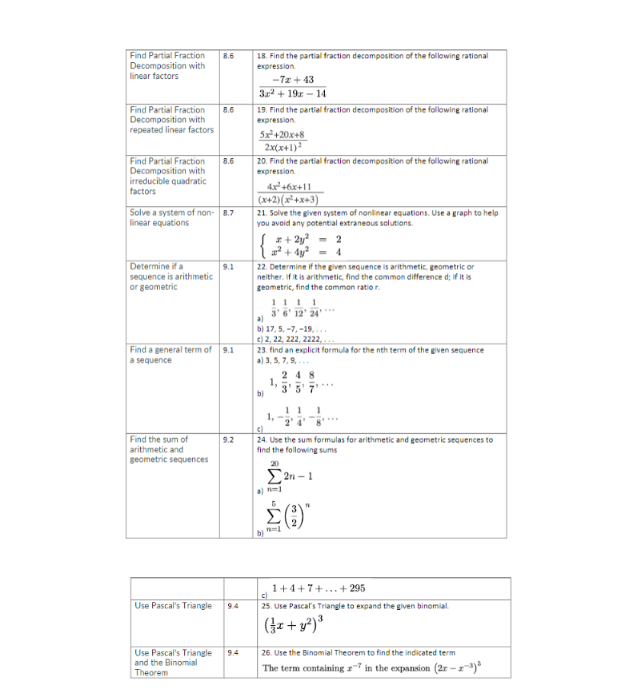
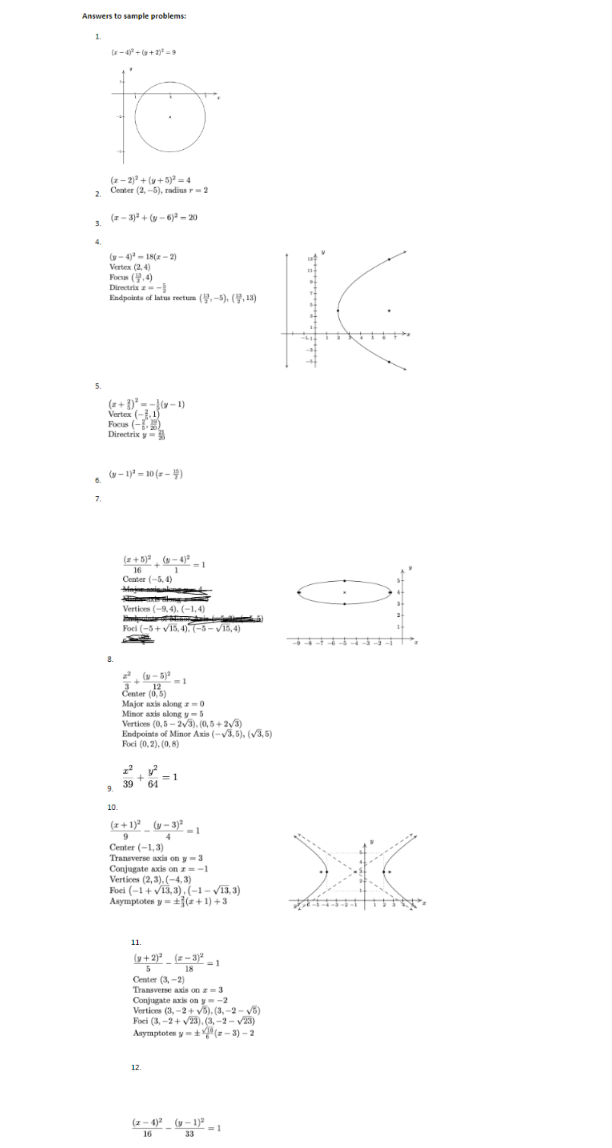
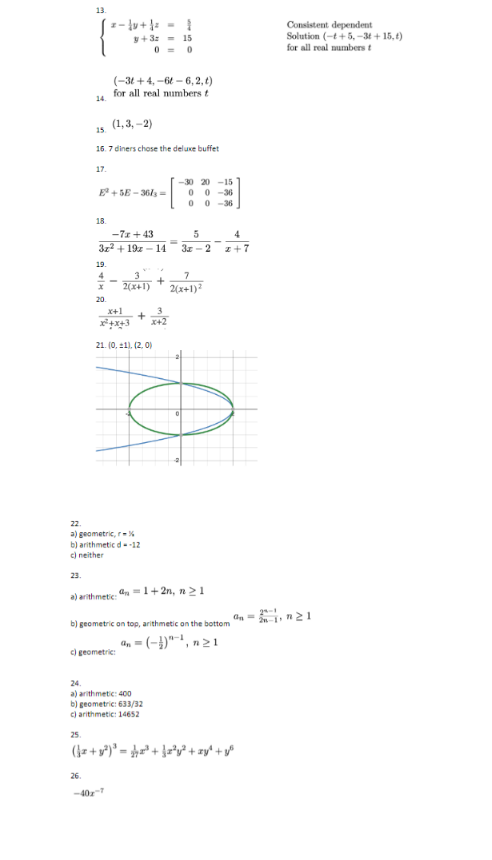
Objective Section Sample Problem Find the standard 7.2 1. Find the standard equation of the circle and then graph it. equation of a circle Center (4, -2), radius 3 and graph it Complete the square in 7.2 2. Complete the square in order to put the equation into standard order to put the form. Identify the center and the radius. equation of a circle into standard form x? - 4x + y' + 10y = -25 Find the equation of a 7.2 3. Find the standard equation of the circle which satisfies the given circle criteria center (3, 6), passes through (-1,4) Graph the equation of 7.3 4. Graph the equation of a parabola. Identify vertex, directix and a parabola. Identify focus vertex, directix and (y - 4)? = 18(z - 2) focus Write equation of 7. 5. Put the equation into standard form and identify the vertex, focus parabola in standard and directrix form 2523 +20x + by - 1 =0 Find the equation of 7. 6. Find an equation for the parabola which fits the given criteria the parabola Focus (10, 1), directrix r = 5 Graph an ellipse. 7.4 7. Graph the ellipse. Find the center, the vertices and the foci. Identify center, (z +5)2 (v - 4)2 vertices and foci _ =1 16 Write equation of 7.4 8. Put the equation in standard form. Find the center, the vertices, and ellipse In standard the foci. form 12x2 + 3y2 - 30y + 39 = 0 Find the equation of 7.4 9. find the standard form of the equation of the ellipse which has the an ellipse given properties. Foci (0, +5), Vertices (0, +8). Graph a hyperbola. 7.5 10. Find the center, the vertices, the foci and the equations of the Identify center, asymptotes. Graph the hyperbola. vertices, foci and asymptotes (s +1)2 (y -3)2 -=1 9 4 Write the equation of 7.5 13. Put the equation in standard form. Find the center, the vertions, the hyperbola in the foci and the equations of the asymptotes. standard form 18y' - 5x3 + 72y + 30r - 63 = 0 Find the equation of 7.5 12. find the standard form of the equation of the hyperbola which has the hyperbola the given properties. Vertex (0, 1), Vertex (8, 1), Focus (-3, 1) Put system of equation 13. Put system of equation in triangular form. Identify type of solution as consistent independent, consistent dependent, or inconsistent in triangular form. Identify type of solution 4x- y+2 - 5 as consistent 20+ 63 = 30 independent, consistent dependent, or inconsistent Determine the 14. Using the augmented matric solutions of a system ") How many variables does this system of equations have? of equations from an 6) Write the equations from each row of the matrix augmented matrix c) Determine the solution of the corresponding system of linear equations or state that the system is inconsistent. 003 010 -6 2 Solve a system of 15. Solve the systems of linear equations using Gaussian elimination. equations using for dependent systems give solution using a parameter Gaussian Elimination I-y+2 = -4 -3x + 2y + 42 -5 - by + 22 - -18 Solve application 16. It's time for a meal at our local buffet, 22 diners (5 of whom were problems using children] feasted for $162.25, before taxes. If the kids buffet is $4 50, systems of equations the basic buffet is $7.50, and the deluxe buffet (with crab legs) is $9.25, find out how many diners chose the deluxe buffet. Perform operations on 83 17. Use the matrix matrices such as scalar multiplication, matrix multiplication, addition and subtraction, exponents To calculate E" + 5E - 36/sFind Partial Fraction B.6 18. Find the partial fraction decomposition of the following rational Decomposition with expression. linear factors -72 + 43 3x2 + 191 - 14 Find Partial Fraction 19. Find the partial fraction decomposition of the following rational Decomposition with expression. repeated linear factors 5x +20x+8 2x(x+1)3 Find Partial Fraction B.6 20. Find the partial fraction decomposition of the following rational Decomposition with expression irreducible quadratic factors Ax +hx+11 (x+2)(x'4x+3) Solve a system of non- 8.7 21. Solve the given system of nonlinear equations. Use a graph to help linear equations you avoid any potential extraneous solutions : + 2y' 2 s' + dy Determine if a 9.1 22. Determine if the given sequence is arithmetic, geometric or sequence is arithmetic neither. If it is arithmetic, find the common difference d; If it is or geometric geometric, find the common ratio r. 1 1 1 1 aj 3'6'12 2417 b| 17. 5, -7, -19, . . . () 2, 22, 222, 2222, ... Find a general term of 9.1 29. find an explicit formula for the nith term of the given sequence a sequence # 3,5. 7, 9, ... 2 48 bj 1 Find the sum of 24. Use the sum formulas for arithmetic and geometric sequences to arithmetic and find the following sums geometric sequences 2n - 1 bn=l 1+4+7+ ...+295 C Use Pascal's Triangle 94 25. use Pascal's Triangle to expand the given binomial Use Pascal's Triangle 94 26. Use the Binomial Theorem to find the indicated term and the Binomial Theorem The term containing a" in the expansion (2r - x-3)"Answers to sample problems: 1. (x -4)+(+1 =9 (x - 2)3 + (#+5)) =4 2. Center (2, -5), radius r = 2 3. (2-3) + (1-6) - 20 ( - 4)' - 18(3 -2) Vertex (2,4) Focus (4.4) Directrix z - - Endpoints of latus rectums ( 1. -5), (1, 13) 5. (#+ 1)' =-16-1) Vertex (- 1.1) Focus (-1.8) Directrix 6. ( -1) = 10(2- 4) 7. (2+5) (0-43 16 Center (-5. 0) Vertices (-9.4). (-1.4) Ford (-5 + v15, 4). (-5 - v15,4) (-5)7 = 1 Center (0, 5) Major axis along = = 0 Minor axis along y = 5 Vertices (0,5 - 2v3). (0,5 + 2v/3) Endpoints of Minor Axis (- v3,5), (v3.5) Foci (0. 2). (0, 8) 30 =1 64 9. 10 (2+1) (y-3) 9 - 1 Center (-1,3) Transverse axis on y = 3 Conjugate axis on a = =1 Vertices (2,3). (-4,3) Foci (-1 + 13,3), (-1 - V13,3) Asymptotes y = (z + 1) +3 11. (y+2) (z -3)3 18 Center (3, -2) Transverse axis on a = 3 Conjugate axis on y = -2 Vertices (3, -2+ v5).(3, -2 - v6) Fori (3, -2 + 23), (3, -2 - v23) Asymptotes y = 1 0(x -3) -2 12. (x -4)2 (v-1)3 =1 16 3313. Consistent dependent 1 + 3: = 15 Solution (- +5, -31 + 15,f) 0 = for all real numbers (-34 + 4, -6t - 6,2, t) 14. for all real numbers 15 (1,3, -2) 16. 7 diners chose the deluxe buffet 17 -30 20 -15 0 0 -3 0 -36 18 -71 +43 3x3 + 19x - 14 3x - 2 2+7 19 4 3 2(X+1) Mx+1) ? x+1 + 3 x+x+3 x42 21. [0, =11. (2, 0) 22 a) geometric, r = % bj arithmetic d = -12 c) neither 21 a) arithmetic:" On =1+2n, n 21 bj geometric on top, arithmetic on the bottom 1, n21 On = (-1)" cl geometric: 24 a) arithmetic: 400 bj geometric: 633/32 cj arithmetic: 14652 25 76 -401-T