Question: On a probability space we are given an increasing filtration Fn. Let Yn be a sequence of random variables such that Y, is Fn-1-measurable Vn.

On a probability space we are given an increasing filtration Fn. Let Yn be a sequence of random variables such that Y, is Fn-1-measurable Vn. Let X, be a (L') Fn-martingale. Prove that, if Yn is uniformly bounded, then the sequence

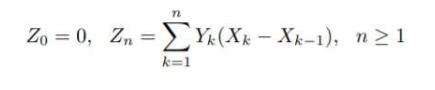Zo = 0, Zn = (X - X-1), 21 k=1 is a martingale. Show the the result is also true if Xn and Yn are L2-martingales.

Zo = 0, Zn = (X - X-1), 21 k=1

Step by Step Solution

★★★★★

3.34 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

SOLUTION GIVEN INFORMATION Inorder simplify prior explanation we will use the following definition of a test Although the definition seems to be extremely abstract the concepts will become more famili... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let Xn be a sequence of random variables that converges in distribution to a random variable X. Let Yn be a sequence of random variables with the property that for any finite number c, Show that for...

Let X and Y be independent random variables such that log(X) has the normal distribution with mean 1.6 and variance 4.5 and log(Y) has the normal distribution with mean 3 and variance 6. Find the...

Let Zn, n 1, be a sequence of random variables and c a constant such that, for each > 0, P{|Zn c| > }0 as n. Show that, for any bounded continuous function g, E[g(Zn)]g(c) as n

ANSWER GIVING STEPS Explain; How do you identify an overflow condition when you add two numbers in 1's complement form? 5.7 Explain the procedure for adding two numbers in 1's complement form. As an...

Growth slowdowns and stock market crashes, donated by Rodolfo Manuelli32 Consider a simple one-tree pure exchange economy. The only source of consumption is the fruit that grows on the tree. This...

2. Health Canada researchers have found that on average, Canadian university students get 90 minutes of aerobic exercise per week with a standard deviation of 20 minutes. (These times are normally...

GENERAL INFORMATION The objective of this project is to analyse the information about young employees in Tasmania and to discuss issues related to relationships between employees wages, abilities and...

Topic: RANDOM VARIABLES AND PROBABILITY DISTRIBUTION MELCs: -illustrate random variable distinguish between a discrete and continuous random variable -find the possible values of a random variable...

Solve the questions in the attachment. 1 Let X and Y have joint density function given by: f(x, y)=c(x+ 3y) 0 0.5). .2 The continuous random variables X, Y have the bivariate PDF: style f(x, y) =2...

Create a Word document and answer the following question. What is the effect of cultural commoditization and transformation on local traditions and customs? Give an example. Please check Chapter 4 in...

a. Can you propose some reasons that herpes simplex and zoster viruses are carried primarily in ganglia? b. What mechanism might account for reactivation of these viruses by various traumatic events?

f Gordo X G Gordo x O Mail M (no su X The M X SB NIST C X W Gordo X BibMe X SST ALEKS X Rb Welco X E Untitle X in Gordo X Cenga X...

You have just been hired as the director of operations for Reid Chocolates, a purveyor of exoeptionally fipe candies. Reld Chocolates is evaluating a vitchen ingul under consideration for its recipe...

On page 50, we noted that the growth rate of per capita GDP in the united tates between 1870 and 1929 was slightly lower than 2%. While the growth rate between 1950 and 2012 was slightly higher....

Calculate the 5-day BOD of a domestic wastewater based on the following data: volume of wastewater added to 300-ml bottle = 6.0 ml, initial DO = 8.1 mg/1,5-day DO = 4.2 mg/1. What is the ultimate BOD...

Determine the domain of the following functions: f(x) = ?x + 2, g(x) = x 2 + 4 / x + 5

A manufacturing company wishes to determine how many of two products they should produce in order to maximize total profit. The labor and material requirements and the contribution to profit for each...

1. Compute the difference quotient f (x + h) f (x) for each function below. h (a) f(x) = 5 2x (b) f(x) = 3x 2 x 6 1 2. Compute the quotient f (b) f (a) for the following function ba (a) f(x) = ...

Based upon the Court's decision in Lockyer v. Andrade, "three-strikes" laws may: Group of answer choices be unconstitutional in certain situations. not be used for nonviolent offenses. not be used in...

Let \((\Omega, \mathscr{A}, P)\) be a probability space and let \(\left(X_{n}ight)_{n \in \mathbb{N}}\) be a sequence of independent identically distributed random variables such that...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Solve the following kindly . Suppose we throw a needle on a large sheet of paper, on which horizontal lines are drawn, which are at needle-length apart (see also Exercise 21.16). Choose one of the...

Question 8 Let (Xn)neNo be a sequence of bounded random variables and consider the filtration (Fn)nen, defined by Fn := o(Xo, X1, . . ., Xn), n E No. Assume that for each n E No we have EXn+1 |Fn] =...

S Markov chains in continuous time. Let E be countable and G D .G.x; y//x;y2E a matrix satisfying the properties (i) G.x; y/ 0 for x y, (ii) a.x/ WD G.x; x/ (iii) a WD supx2E a.x/ We construct a...

the green line is a question. thank you Consider a standard binomial model of a risky asset where there are two states of nature, the UP state and the DOWN state. The former is denoted by U and the...