Question: One major idea that we have explored in this module is that derivatives allow us to make specic claims about the changes to multiple quanties

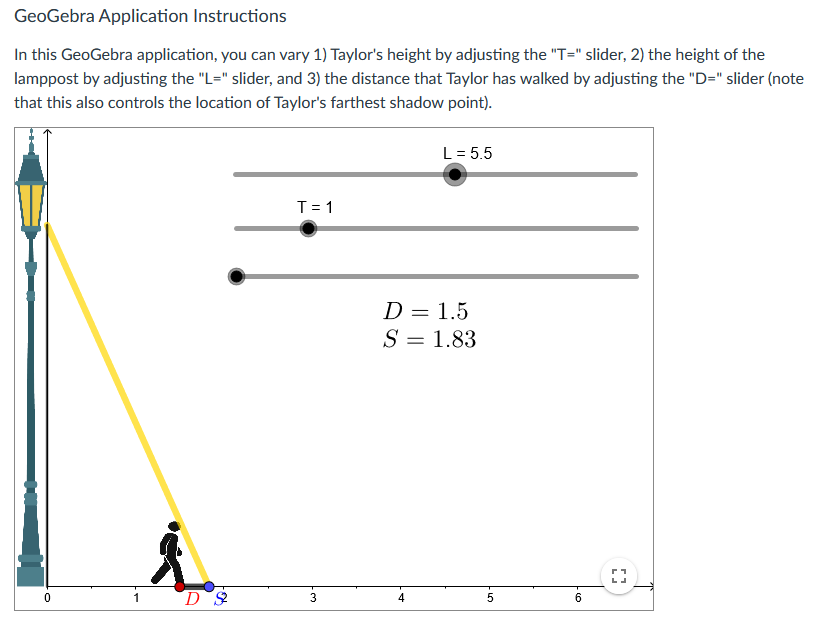


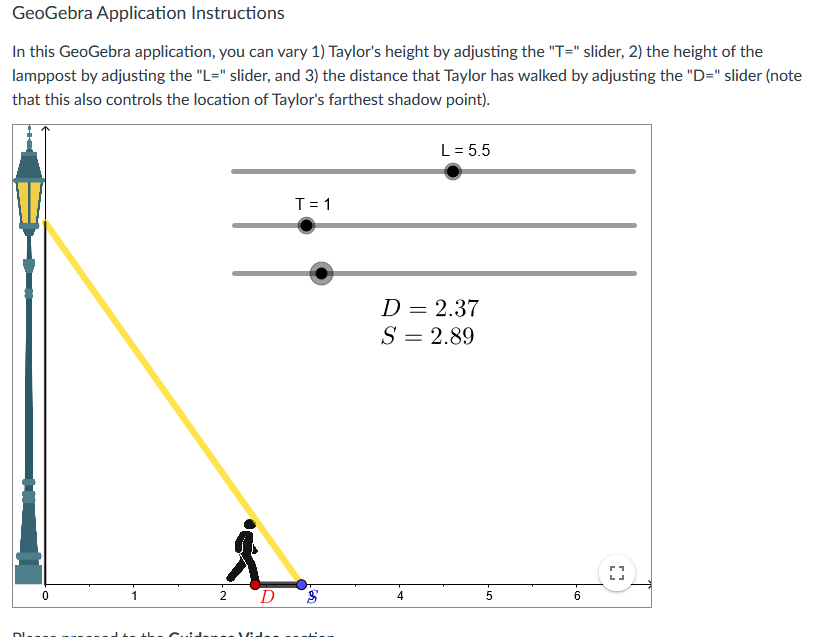
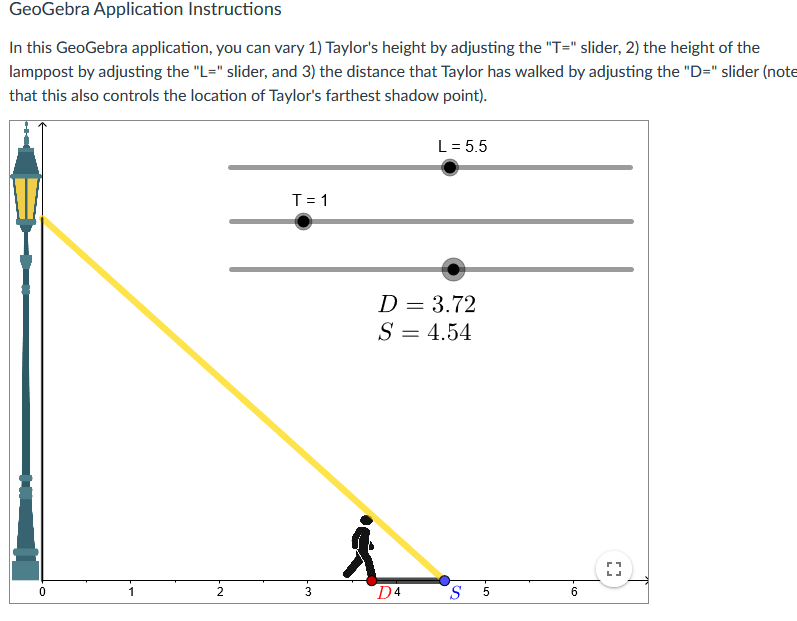
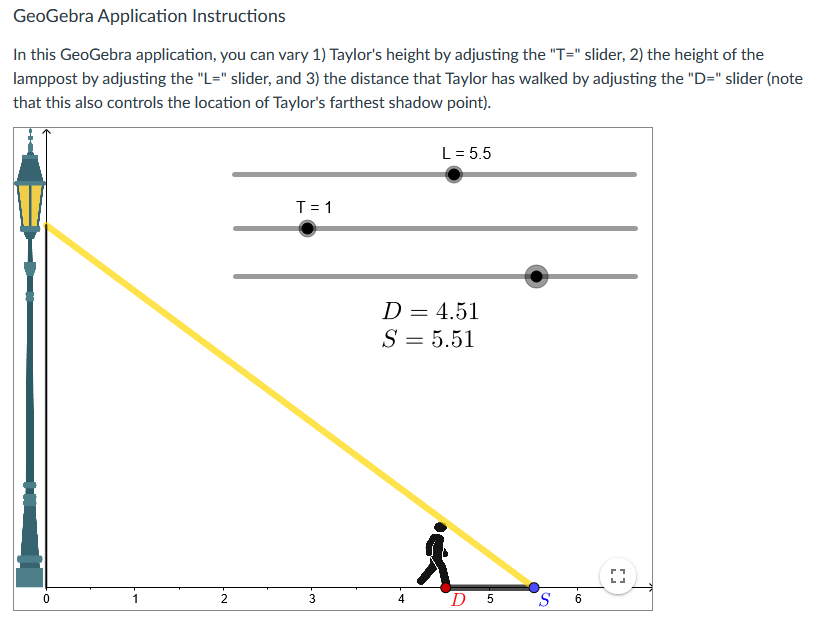
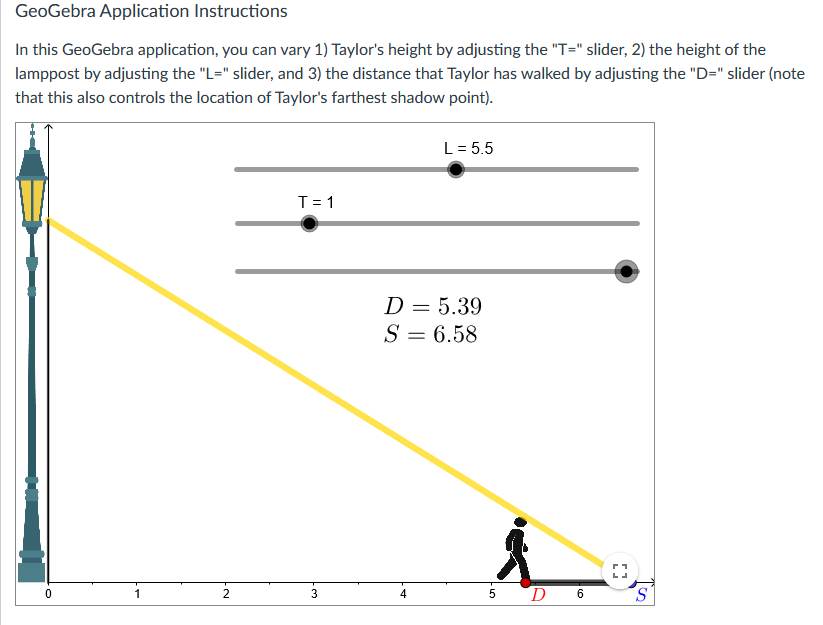

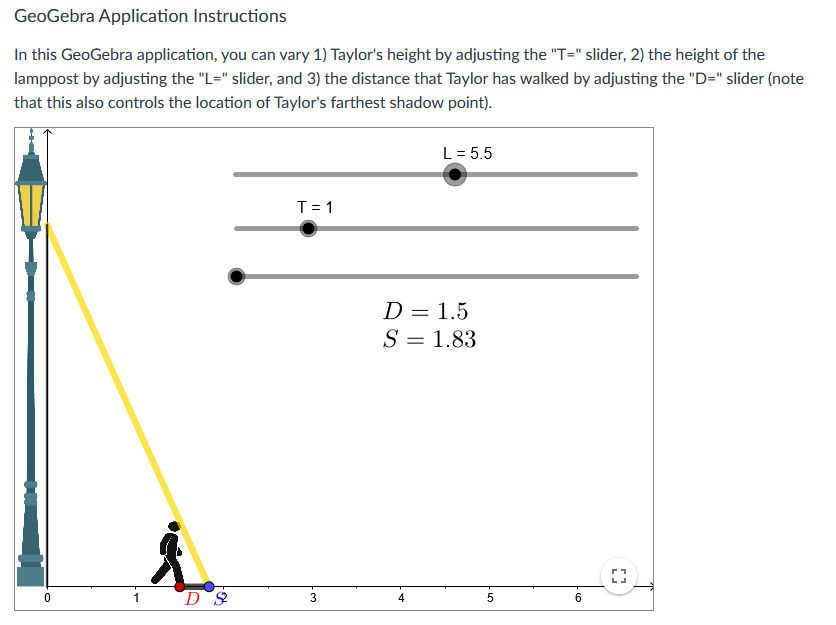


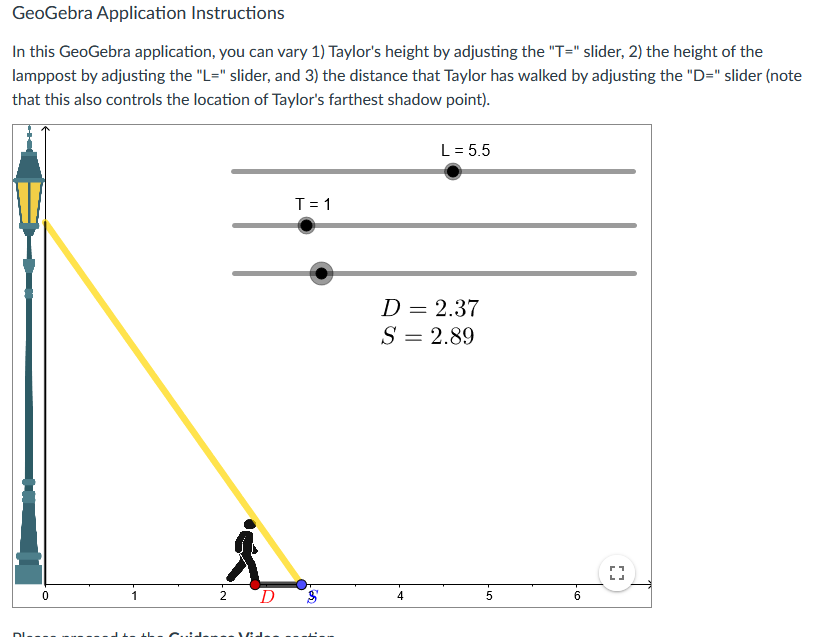
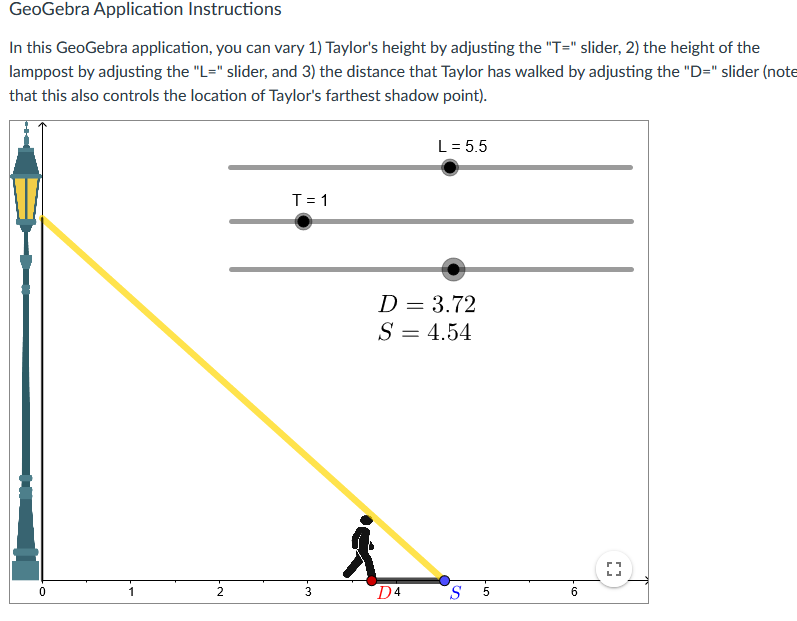
![you can vary 1] Taylor's height by adjusting the "T=" slider, 2}](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667c488c17db0_068667c488c04713.jpg)
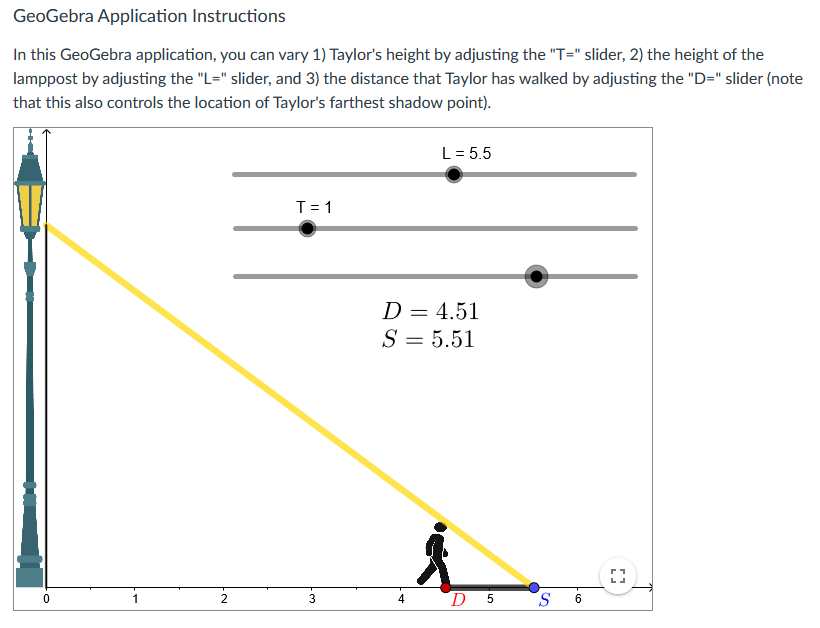
One major idea that we have explored in this module is that derivatives allow us to make specic claims about the changes to multiple quanties that co-vary in the context of an unfolding dynamic process that we observe. Making these claims requires that we attend to the relationships between multiple related quantities as they co-vary, and then to determine time-specic and time-independent rates of change using the differentiation tools that we have been gaining over time. In this assessment, you will analyze an increasingly complex contextual problem involving a person, Taylor, walking away from a lamppost. As with last module week's conceptual assessment, you will be using the random value generator to situate your initial work on this problem: Generate New Values L255 Dvera ll Goal Your goal is to compare Taylor's distance from the lamppost and the length of his shadow. Specically, your overall goal is to determine {and then justify} the conditions by which Taylor walks away from the lamppost faster than the rate at which his shadow is growing. GeoGebra Application Instructions In this GeoGebra application, you can vary 1] Taylor's height by adjusting the "T=" slider, 2} the height of the lamppost by adjusting the "L=" slider, and 3} the distance that Taylor has walked by adjusting the "D=" slider {note that this also controls the location of Taylor's farthest shadow point}. First, you will need to determine the relationship between Taylor's distance from the lamppost and the length of his shadow for specific values of L and T using the applet. This will give you some initial insight into the relationships at play as Taylor walks forward. Specifically, Taylor's distance from the lamppost and shadow length determine a constant rate of change relationship. Generate a specific T-value and a specific L-value using the random value generator, and then determine the constant rate of change between Taylor's distance and his shadow length using the "D=" slider. You need to not only determine the specific constant rate of change but also justify the correctness of the determined constant rate with descriptions of how you gained relevant information from the applet. Your justification should appeal to the definition of a constant rate of change relationship. (Hint: Remember that constant rates of change involve comparing two quantities' related changes, so you'll want to measure and compare the changes in these two quantities.)You now have the freedom to vary L and T as desired. Notice that the parameters of this problem are: 1) the height of the lamppost, L, 2) Taylor's height, T, and 3) Taylor's distance, D, at any moment in time as they travel between 1.5 and 5.5 meters from the lamppost. Your goal is to analyze the relationships between these three variables with respect to the comparative growth rate of Taylor's distance and shadow length. Specifically, depending on the fixed values of T and L, Taylor might walk faster than his shadow grows, at the same speed as the growth rate of his shadow, or his shadow might grow faster than they walk. You are to determine the relationship between the relevant parameters that specifically result in Taylor walking faster than his shadow is growing. This relationship might involve comparisons of T and L values such as with a difference or a ratio, or might involve other operations such as summation or multiplication. For instance, Taylor might walk faster than his shadow grows so long as T+L is greater than 5. Your answer should include a justification from your manipulations of the applet and from constructing and interpreting a related rates equation.GeoGebra Application Instructions In this GeoGebra application, you can vary 1) Taylor's height by adjusting the "T=" slider, 2) the height of the lamppost by adjusting the "L=" slider, and 3) the distance that Taylor has walked by adjusting the "D=" slider (note that this also controls the location of Taylor's farthest shadow point). L = 5.5 T = 1 D = 2.37 S = 2.89 N- D Un -GeoGebra Application Instructions In this GeoGebra application, you can vary 1) Taylor's height by adjusting the "T=" slider, 2) the height of the lamppost by adjusting the "L=" slider, and 3) the distance that Taylor has walked by adjusting the "D=" slider (not that this also controls the location of Taylor's farthest shadow point). L = 5.5 T = 1 D = 3.72 S = 4.54 D4 SGeoGebra Application Instructions In this GeoGebra application, you can vary 1) Taylor's height by adjusting the "T=" slider, 2) the height of the lamppost by adjusting the "L=" slider, and 3) the distance that Taylor has walked by adjusting the "D=" slider (note that this also controls the location of Taylor's farthest shadow point). L = 5.5 T = 1 D = 4.51 S = 5.51 N - D 5 S 0) -GeoGebra Application Instructions In this GeoGebra application, you can vary 1) Taylor's height by adjusting the "T=" slider, 2) the height of the lamppost by adjusting the "L=" slider, and 3) the distance that Taylor has walked by adjusting the "D=" slider (note that this also controls the location of Taylor's farthest shadow point). L = 5.5 T =1 D = 5.39 S = 6.58 1 N. 4 5 D 6 S
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


