Only need the work shown for the answers with the red corners, thank you

1) c-f

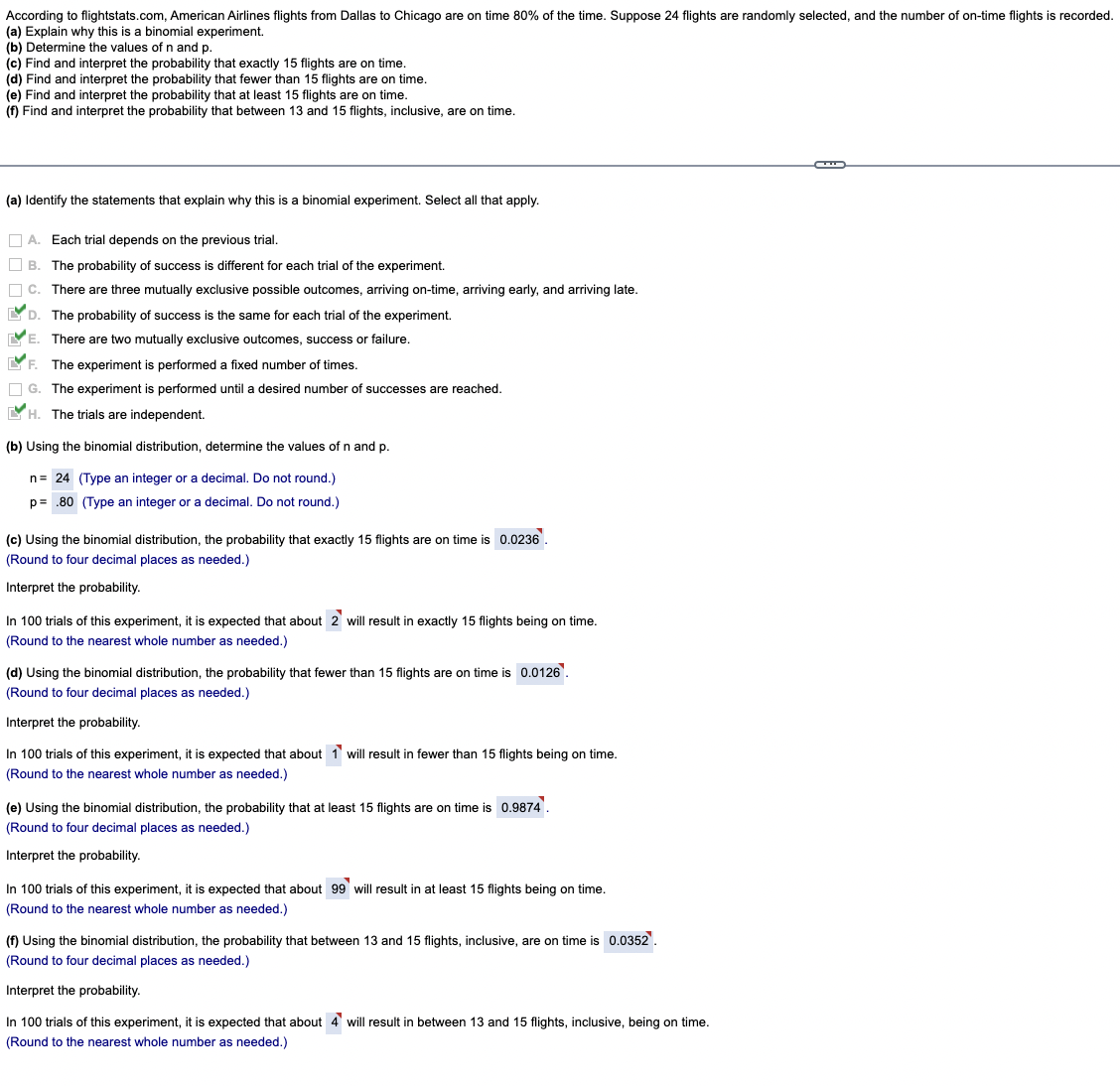
According to flightstats.com, American Airlines flights from Dallas to Chicago are on time 80% of the time. Suppose 24 flights are randomly selected, and the number of on-time flights is recorded. (a) Explain why this is a binomial experiment. (b) Determine the values of n and p. (c) Find and interpret the probability that exactly 15 flights are on time. 'd) Find and interpret the probability that fewer than 15 flights are on time. (e) Find and interpret the probability that at least 15 flights are on time. (f) Find and interpret the probability that between 13 and 15 flights, inclusive, are on time. (a) Identify the statements that explain why this is a binomial experiment. Select all that apply. A. Each trial depends on the previous trial. B. The probability of success is different for each trial of the experiment. C. There are three mutually exclusive possible outcomes, arriving on-time, arriving early, and arriving late. Y D. The probability of success is the same for each trial of the experiment. YE. There are two mutually exclusive outcomes, success or failure. F. The experiment is performed a fixed number of times. G. The experiment is performed until a desired number of successes are reached. H. The trials are independent. (b) Using the binomial distribution, determine the values of n and p. n= 24 (Type an integer or a decimal. Do not round.) p= .80 (Type an integer or a decimal. Do not round.) (c) Using the binomial distribution, the probability that exactly 15 flights are on time is 0.0236. (Round to four decimal places as needed.) Interpret the probability In 100 trials of this experiment, it is expected that about 2 will result in exactly 15 flights being on time. (Round to the nearest whole number as needed.) (d) Using the binomial distribution, the probability that fewer than 15 flights are on time is 0.0126 . (Round to four decimal places as needed.) Interpret the probability. In 100 trials of this experiment, it is expected that about 1 will result in fewer than 15 flights being on time. (Round to the nearest whole number as needed.) (e) Using the binomial distribution, the probability that at least 15 flights are on time is 0.9874 . (Round to four decimal places as needed.) Interpret the probability In 100 trials of this experiment, it is expected that about 99 will result in at least 15 flights being on time. Round to the nearest whole number as needed.) (f) Using the binomial distribution, the probability that between 13 and 15 flights, inclusive, are on time is 0.0352 (Round to four decimal places as needed.) Interpret the probability In 100 trials of this experiment, it is expected that about 4 will result in between 13 and 15 flights, inclusive, being on time. (Round to the nearest whole number as needed.)Suppose that the lifetimes of light bulbs are approximately normally distributed, with a mean of 57 hours and a standard deviation of 3.5 hours. With this information, answer the following questions. (a) What proportion of light bulbs will last more than 61 hours? (b) What proportion of light bulbs will last 52 hours or less? (c) What proportion of light bulbs will last between 57 and 61 hours? (d) What is the probability that a randomly selected light bulb lasts less than 46 hours? (a) The proportion of light bulbs that last more than 61 hours is 0.1265 . (Round to four decimal places as needed.) (b) The proportion of light bulbs that last 52 hours or less is .0766. (Round to four decimal places as needed.) (c) The proportion of light bulbs that lasts between 57 and 61 hours is .3735 . (Round to four decimal places as needed.) (d) The probability that a randomly selected light bulbs lasts less than 46 hours is 0.0008 . (Round to four decimal places as needed.)