only questions 3 and 4

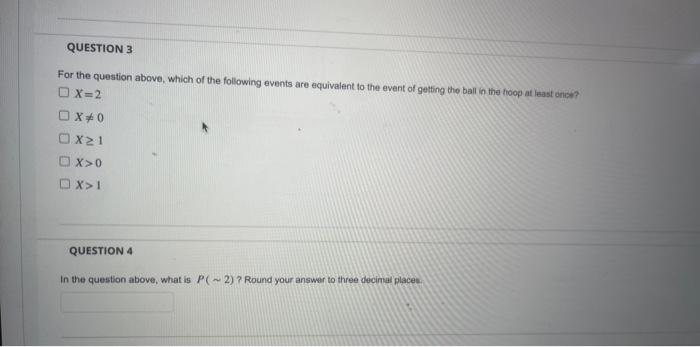
Consider a model to be a probability model if it satisfies the Axioms of Probability and identify which of the models balow ace probabiity models a) Rolling a six-sided dee, where the probability of each value landing face-up is: P(1)=1/6P(2)=0P(3)=1/2P(4)=0P(5)=1/6P(6)=1/3 b) Dealing a single card from a deck, where the probability of being dealt each face value is: P( Heart )=16/52P(Club)=14/52P( Diamond )=10/52P( Spade )=12/52 Both a and b are probability models. Only a is a probability model Only b is a probability model. Neither a nor b are probability models. QUESTION 2 Suppose that John shoots two basketbalis at a basketball hoop and let X be the number of times he geta the ball in the hoop. The sampoe space of a probubility model for this is then S={0,1,2) and the probabilities of each outcome are. P(0)=1/16P(1)=7/8P(2)=1/16 Is this probability model discrete or continuous? Diecrete Continuous For the question above, which of the following events are equivalent to the event of getting the ball in the foop at least onick? x=2x=0x1x>0x>1 QUESTION 4 In the question above, what is P(2) ? Round your answer to three decinkal places