OPERATIONS MANAGEMENT

HELP ME FROM QUESTION 2 TO QUESTION 4

1) Formulate and solve a linear program for this problem. Please provide all your model formulations and solutions.

MY SOLUTIONS ARE:

YOUR QUESTIONS START FROM HERE :

2) What is your resulting recommendation to the school board? Preparee a managerial report to the EG.

3) Do sensitivity analysis, please include your sensitivity analysis, and answer the following questions:

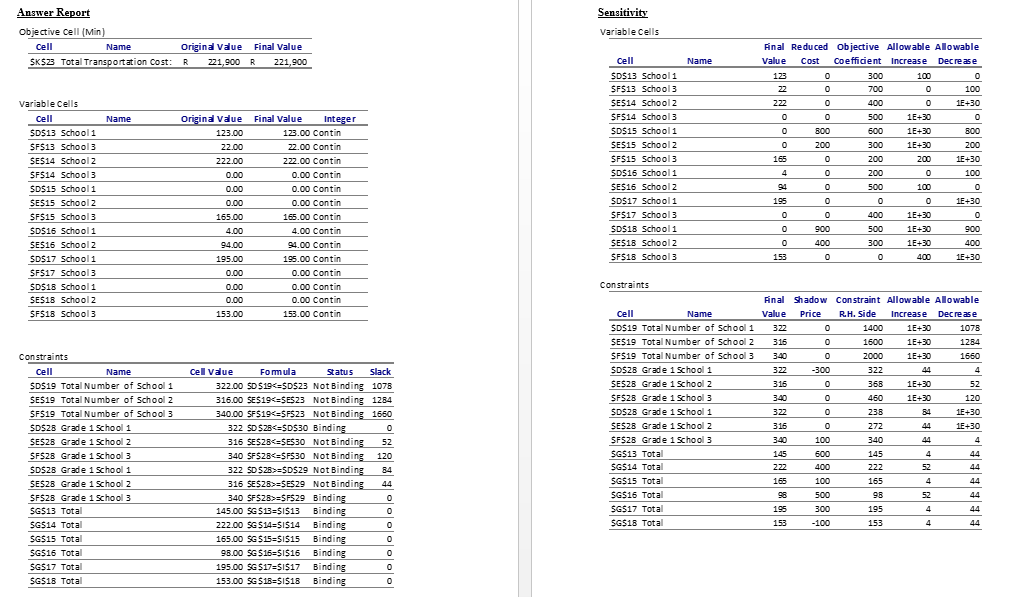
(a) Use the sensitivity report to check how much the transport from area 2 to school 2 can increase ( assuming no other cost increases) before the current optimal solution would no longer be optimal. If the allowable increase is less or equal to 50 percent use solver to find the new solution with a 55 percent increase.

(b) What is the reduced cost of x11, what does this mean?

(c) How many more than the 17 percent of learners in school 1 are grade ones? (row 8)

d) The school board has the option of adding portable classrooms to increase the capacity of one or more schools. Each portable classroom holds 20 students and has a lease cost of R2 500 per month. For each school use the corresponding shadow price from the sensitivity report to determine whether it would be worthwhile to add any portable classrooms.

After seeing your recommendation, the school board expresses concern about all the splitting of learners from residential areas among different schools. They indicate that they would like to keep each neighborhood together. They relax their rule that about the 17% and 23% percent of the school may be grade ones to be able to find a solution.

4) Adjust your recommendation to enable each area to be assigned to just one school by formulating a binary integer model for the problem under the current policy of providing transportation for students having to travel more than a km.(The question 1 model.)

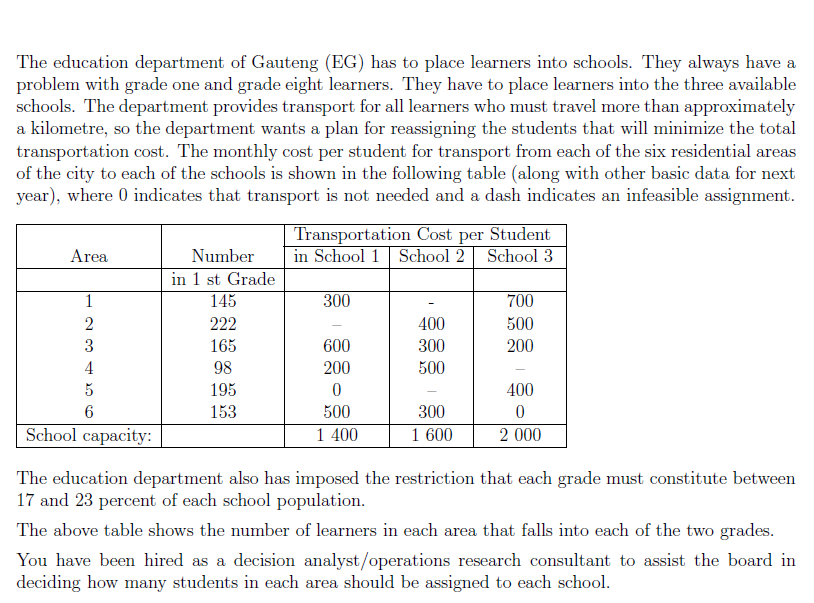
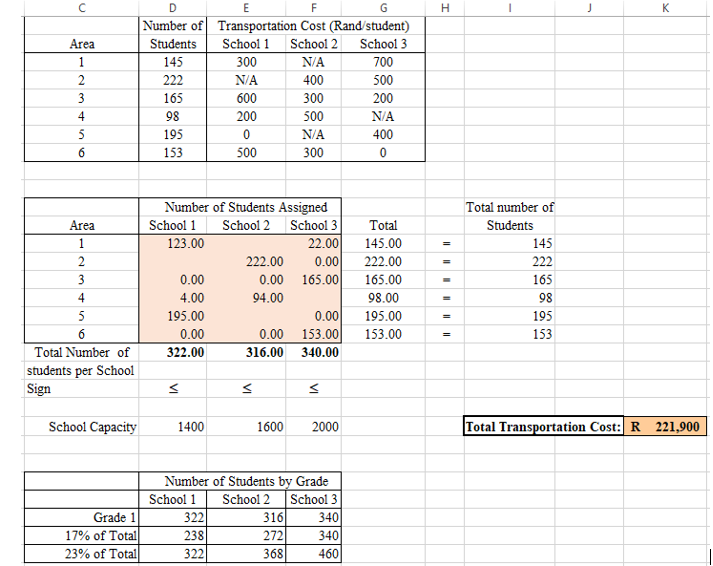
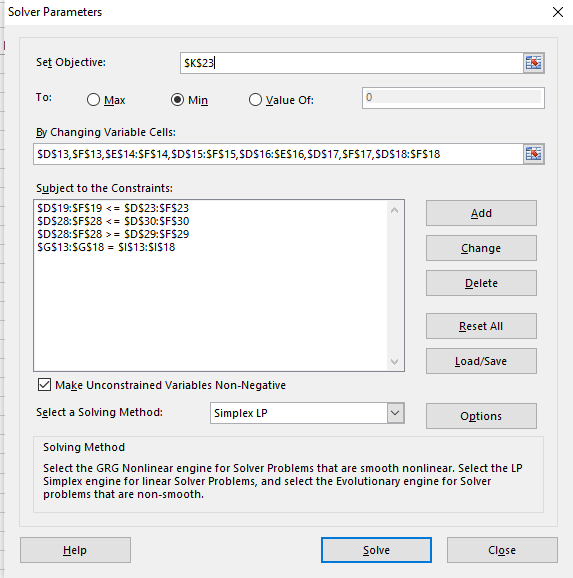
The education department of Gauteng (EG) has to place learners into schools. They always have a problem with grade one and grade eight learners. They have to place learners into the three available schools. The department provides transport for all learners who must travel more than approximately a kilometre, so the department wants a plan for reassigning the students that will minimize the total transportation cost. The monthly cost per student for transport from each of the six residential areas of the city to each of the schools is shown in the following table (along with other basic data for next year), where 0 indicates that transport is not needed and a dash indicates an infeasible assignment. Transportation Cost per Student in School 1 School 2 School 3 Area 300 Number in 1 st Grade 145 222 165 98 195 153 1 2 3 4 5 6 School capacity: 700 500 200 600 400 300 500 200 0 500 1 400 300 1 600 400 0 2 000 The education department also has imposed the restriction that each grade must constitute between 17 and 23 percent of each school population. The above table shows the number of learners in each area that falls into each of the two grades. You have been hired as a decision analyst /operations research consultant to assist the board in deciding how many students in each area should be assigned to each school. = Minimize Z 300x11 + 700x13 + 400X22 + 500X23 + 600X31 + 300X32 + 200x33 + 200X41 + 500X42 + 0x51 + 400X53 +500X61 + 300X62 +0X63 Under Constraint: X11 + X13 = 145 X22 + X23 = 222 X31 + X32 + X33 = 165 X41 + x42 = 98 X51 + X53 = 195 X61 + X62 + X63 = 153 X11 + X31 + X41 + X51 + X61 =SD$29 Not Binding 84 316 SES2B>=SE$29 Not Binding 44 340 SF528>=5F529 Binding 0 145.00 SG $13=51513 Binding 0 222.00 SG $14=51514 Binding o 165.00 SG $15-51515 Binding 0 98.00 SG $16=51516 Binding 0 195.00 SG $17=$I$17 Binding 0 153.00 SG $18=SI$18 Binding 0 Cell Name $D$19 Total Number of School 1 SE519 Total Number of School 2 SF519 Total Number of School 3 SD$28 Grade 1 School 1 SE$28 Grade 1 School 2 SF$28 Grade 1 School 3 SD$2B Grade 1 School 1 SE528 Grade 1 School 2 SF52B Grade 1 School 3 SGS13 Total SGS14 Total SG$15 Total SG$16 Total SGS17 Total SGS18 Total Anal Shadow Constraint Allowable Alowable Value Price R.H. Side Increase Decrease 322 0 1400 1E+30 1078 316 0 1600 1E+30 1284 340 0 2000 1E+30 1650 322 -300 322 44 4 316 0 368 1E+30 52 340 0 460 1E+30 120 322 0 238 84 1E+30 316 0 272 44 1E+30 340 100 340 44 4 145 600 145 4 44 222 400 222 52 44 165 100 165 4 44 98 500 98 52 44 195 300 195 4 44 153 -100 153 4 44 Solver Parameters Set Objective: SK$23 To: Max Min Value Of: 0 By Changing Variable Cells: $D$13,5F$13, SES14:$F$14,SD$15:$F$15,SD$16:$E$16, SD$17,5F517,SD$18:$F$18 Subject to the Constraints: SD$19:$F$19 = SDS29:$F$29 SG$13:$G$18 - SI$13:SI$18 Add Change Delete Reset All Load/Save Make Unconstrained variables Non-Negative Select a Solving Method: Simplex LP Options Solving Method Select the GRG Nonlinear engine for Solver Problems that are smooth nonlinear. Select the LP Simplex engine for linear Solver Problems, and select the Evolutionary engine for Solver problems that are non-smooth. Help Solve Close The education department of Gauteng (EG) has to place learners into schools. They always have a problem with grade one and grade eight learners. They have to place learners into the three available schools. The department provides transport for all learners who must travel more than approximately a kilometre, so the department wants a plan for reassigning the students that will minimize the total transportation cost. The monthly cost per student for transport from each of the six residential areas of the city to each of the schools is shown in the following table (along with other basic data for next year), where 0 indicates that transport is not needed and a dash indicates an infeasible assignment. Transportation Cost per Student in School 1 School 2 School 3 Area 300 Number in 1 st Grade 145 222 165 98 195 153 1 2 3 4 5 6 School capacity: 700 500 200 600 400 300 500 200 0 500 1 400 300 1 600 400 0 2 000 The education department also has imposed the restriction that each grade must constitute between 17 and 23 percent of each school population. The above table shows the number of learners in each area that falls into each of the two grades. You have been hired as a decision analyst /operations research consultant to assist the board in deciding how many students in each area should be assigned to each school. = Minimize Z 300x11 + 700x13 + 400X22 + 500X23 + 600X31 + 300X32 + 200x33 + 200X41 + 500X42 + 0x51 + 400X53 +500X61 + 300X62 +0X63 Under Constraint: X11 + X13 = 145 X22 + X23 = 222 X31 + X32 + X33 = 165 X41 + x42 = 98 X51 + X53 = 195 X61 + X62 + X63 = 153 X11 + X31 + X41 + X51 + X61 =SD$29 Not Binding 84 316 SES2B>=SE$29 Not Binding 44 340 SF528>=5F529 Binding 0 145.00 SG $13=51513 Binding 0 222.00 SG $14=51514 Binding o 165.00 SG $15-51515 Binding 0 98.00 SG $16=51516 Binding 0 195.00 SG $17=$I$17 Binding 0 153.00 SG $18=SI$18 Binding 0 Cell Name $D$19 Total Number of School 1 SE519 Total Number of School 2 SF519 Total Number of School 3 SD$28 Grade 1 School 1 SE$28 Grade 1 School 2 SF$28 Grade 1 School 3 SD$2B Grade 1 School 1 SE528 Grade 1 School 2 SF52B Grade 1 School 3 SGS13 Total SGS14 Total SG$15 Total SG$16 Total SGS17 Total SGS18 Total Anal Shadow Constraint Allowable Alowable Value Price R.H. Side Increase Decrease 322 0 1400 1E+30 1078 316 0 1600 1E+30 1284 340 0 2000 1E+30 1650 322 -300 322 44 4 316 0 368 1E+30 52 340 0 460 1E+30 120 322 0 238 84 1E+30 316 0 272 44 1E+30 340 100 340 44 4 145 600 145 4 44 222 400 222 52 44 165 100 165 4 44 98 500 98 52 44 195 300 195 4 44 153 -100 153 4 44 Solver Parameters Set Objective: SK$23 To: Max Min Value Of: 0 By Changing Variable Cells: $D$13,5F$13, SES14:$F$14,SD$15:$F$15,SD$16:$E$16, SD$17,5F517,SD$18:$F$18 Subject to the Constraints: SD$19:$F$19 = SDS29:$F$29 SG$13:$G$18 - SI$13:SI$18 Add Change Delete Reset All Load/Save Make Unconstrained variables Non-Negative Select a Solving Method: Simplex LP Options Solving Method Select the GRG Nonlinear engine for Solver Problems that are smooth nonlinear. Select the LP Simplex engine for linear Solver Problems, and select the Evolutionary engine for Solver problems that are non-smooth. Help Solve Close