Operations Research Problem

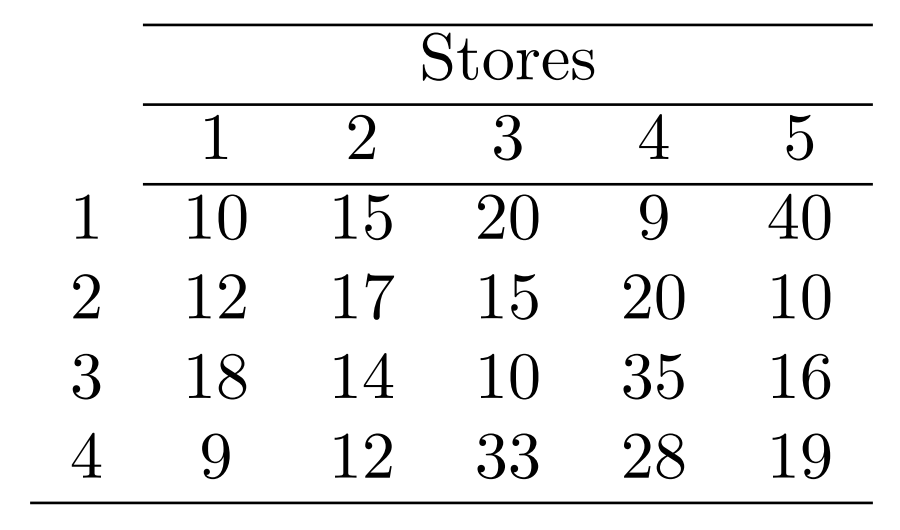
Consider the following integer-linear program which is used to decide which warehouses to open from a set of n potential warehouses, and how to assign m retail stores to the opened warehouses (for receiving supplies). Note that each retail store must be assigned to exactly one warehouse. Each warehouse can serve all the retail stores. Associated with each assignment is a transportation cost cij,i=1,,n,j=1,,m, and associated with opening each warehouse is a fixed cost fi,i=1,,n. We seek to minimize the total cost. This is known as a location-allocation model. Let xij={1,0,ifstorejisassignedtowarehousei,i=1,,n,j=1,,mo/w yi={1,0,ifwarehouseiisopened,i=1,,no/w Then, the location-allocation model is: mins.t.z=i=1nj=1mcijxij+i=1nfiyii=1nxij=1,j=1mxijmyixij{0,1},i=1,,m,yi{0,1},i=1,,n. Assume that n=4,m=5, and that the fixed cost for opening a warehouse is $20,000 for each of four warehouses. The transportation costs for all pairs of warehouses and stores (in thousands) are provided in the table below: \begin{tabular}{cccccc} \cline { 2 - 6 } & \multicolumn{5}{c}{ Stores } \\ \cline { 2 - 6 } 1 & 1 & 2 & 3 & 4 & 5 \\ \cline { 2 - 6 } 2 & 12 & 15 & 20 & 9 & 40 \\ 3 & 18 & 14 & 10 & 20 & 10 \\ 4 & 9 & 12 & 33 & 28 & 19 \\ \hline \end{tabular} 1. For the solution [1,0,0,1] which represents that warehouses 1 and 4 are open, compute the total cost, z(x,y) and describe how you did so. Note that the notation for solutions that we will use uses a 1 to indicate that the corresponding warehouse is open and 0 otherwise. 2. Run Tabu Search for five iterations with tenure period =2, and starting with the solution [1,0,0,1]. A neighborhood here is defined as a solution in which the status of only one warehouse is flipped, i.e., you can flip one warehouse from being open to being closed or vice versa to generate a neighbor (except if that warehouse is on the Tabu list). If a warehouse is flipped from open to closed or vice versa, that warehouse (not the entire solution) should then go on the Tabu list. Use random-walk selection for neighbors. For this part, use the random numbers from seed (1,1), and use them in this order! Show detailed work for every iteration, then at the end of the algorithm, report the best solution found. Random Number Table \begin{tabular}{llllllllll} 13962 & 70992 & 65172 & 28053 & 02190 & 83634 & 66012 & 70305 & 66761 & 88344 \\ 43905 & 46941 & 72300 & 11641 & 43548 & 30455 & 07686 & 31840 & 03261 & 89139 \\ 00504 & 48658 & 38051 & 59408 & 16508 & 82979 & 92002 & 63606 & 41078 & 86326 \\ 61274 & 57238 & 47267 & 35303 & 29066 & 02140 & 60867 & 39847 & 50968 & 96719 \\ 43753 & 21159 & 16239 & 50595 & 62509 & 61207 & 86816 & 29902 & 23395 & 72640 \\ & & & & & & & & & \\ 83503 & 51662 & 21636 & 68192 & 84294 & 38754 & 84755 & 34053 & 94582 & 29215 \\ 36807 & 71420 & 35804 & 44862 & 23577 & 79551 & 42003 & 58684 & 09271 & 68396 \\ 19110 & 55680 & 18792 & 41487 & 16614 & 83053 & 00812 & 16749 & 45347 & 88199 \\ 82615 & 86984 & 93290 & 87971 & 60022 & 35415 & 20852 & 02909 & 99476 & 45568 \\ 05621 & 26584 & 36493 & 63013 & 68181 & 57702 & 49510 & 75304 & 38724 & 15712 \\ & & & & & & & & & \\ 06936 & 37293 & 55875 & 71213 & 83025 & 46063 & 74665 & 12178 & 10741 & 58362 \\ 84981 & 60458 & 16194 & 92403 & 80951 & 80068 & 47076 & 23310 & 74899 & 87929 \\ 66354 & 88441 & 96191 & 04794 & 14714 & 64749 & 43097 & 83976 & 83281 & 72038 \\ 49602 & 94109 & 36460 & 62353 & 00721 & 66980 & 82554 & 90270 & 12312 & 56299 \\ 78430 & 72391 & 96973 & 70437 & 97803 & 78683 & 04670 & 70667 & 58912 & 21883 \\ & & & & & & & & & \\ 33331 & 51803 & 15934 & 75807 & 46561 & 80188 & 78984 & 29317 & 27971 & 16440 \\ 62843 & 84445 & 56652 & 91797 & 45284 & 25842 & 96246 & 73504 & 21631 & 81223 \\ 19528 & 15445 & 77764 & 33446 & 41204 & 70067 & 33354 & 70680 & 66664 & 75486 \\ 16737 & 01887 & 50934 & 43306 & 75190 & 86997 & 56561 & 79018 & 34273 & 25196 \\ 99389 & 06685 & 45945 & 62000 & 76228 & 60645 & 87750 & 46329 & 46544 & 95665 \\ & & & & & & & & & \\ 36160 & 38196 & 77705 & 28891 & 12106 & 56281 & 86222 & 66116 & 39626 & 06080 \\ 05505 & 45420 & 44016 & 79662 & 92069 & 27628 & 50002 & 32540 & 19848 & 27319 \\ 85962 & 19758 & 92795 & 00458 & 71289 & 05884 & 37963 & 23322 & 73243 & 98185 \\ 28763 & 04900 & 54460 & 22083 & 89279 & 43492 & 00066 & 40857 & 86568 & 49336 \\ 42222 & 40446 & 82240 & 79159 & 44168 & 38213 & 46839 & 26598 & 29983 & 67645 \end{tabular} \begin{tabular}{llllllllll} 43626 & 40039 & 51492 & 36488 & 70280 & 24218 & 14596 & 04744 & 89336 & 35630 \\ 97761 & 43444 & 95895 & 24102 & 07006 & 71923 & 04800 & 32062 & 41425 & 66862 \\ 49275 & 44270 & 52512 & 03951 & 21651 & 53867 & 73531 & 70073 & 45542 & 22831 \\ 15797 & 75134 & 39856 & 73527 & 78417 & 36208 & 59510 & 76913 & 22499 & 68467 \\ 04497 & 24853 & 43879 & 07613 & 26400 & 17180 & 18880 & 66083 & 02196 & 10638 \\ & & & & & & & & & \\ 95468 & 87411 & 30647 & 88711 & 01765 & 57688 & 60665 & 57636 & 36070 & 37285 \\ 01420 & 74218 & 71047 & 14401 & 74537 & 14820 & 45248 & 78007 & 65911 & 38583 \\ 74633 & 40171 & 97092 & 79137 & 30698 & 97915 & 36305 & 42613 & 87251 & 75608 \\ 46662 & 99688 & 59576 & 04887 & 02310 & 35508 & 69481 & 30300 & 94047 & 57096 \\ 10853 & 10393 & 03013 & 90372 & 89639 & 65800 & 88532 & 71789 & 59964 & 50681 \\ & & & & & & & & & \\ 68583 & 01032 & 67938 & 29733 & 71176 & 35699 & 10551 & 15091 & 52947 & 20134 \\ 75818 & 78982 & 24258 & 93051 & 02081 & 83890 & 66944 & 99856 & 87950 & 13952 \\ 16395 & 16837 & 00538 & 57133 & 89398 & 78205 & 72122 & 99655 & 25294 & 20941 \\ 53892 & 15105 & 40963 & 69267 & 85534 & 00533 & 27130 & 90420 & 72584 & 84576 \\ 66009 & 26869 & 91829 & 65078 & 89616 & 49016 & 14200 & 97469 & 88307 & 92282 \\ & & & & & & & & & \\ 45292 & 93427 & 92326 & 70206 & 15847 & 14302 & 60043 & 30530 & 57149 & 08642 \\ 34033 & 45008 & 41621 & 79437 & 98745 & 84455 & 66769 & 94729 & 17975 & 50963 \\ 13364 & 09937 & 00535 & 88122 & 47278 & 90758 & 23542 & 35273 & 67912 & 97670 \\ 03343 & 62593 & 93332 & 09921 & 25306 & 57483 & 98115 & 33460 & 55304 & 43572 \\ 46145 & 24476 & 62507 & 19530 & 41257 & 97919 & 02290 & 40357 & 38408 & 50031 \\ & & & & & & & & & \\ 37703 & 51658 & 17420 & 30593 & 39637 & 64220 & 45486 & 03698 & 80220 & 12139 \\ 12622 & 98083 & 17689 & 59677 & 56603 & 93316 & 79858 & 52548 & 67367 & 72416 \\ 56043 & 00251 & 70085 & 28067 & 78135 & 53000 & 18138 & 40564 & 77086 & 49557 \\ 43401 & 35924 & 28308 & 55140 & 07515 & 53854 & 23023 & 70268 & 80435 & 24269 \\ 18053 & 53460 & 32125 & 81357 & 26935 & 67234 & 78460 & 47833 & 20496 & 35645 \end{tabular}