Optimization, BFGS algorithm proof.

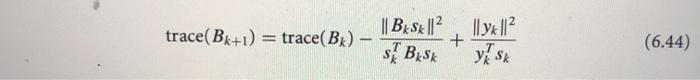
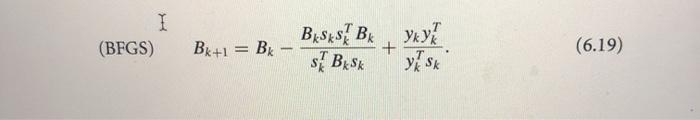
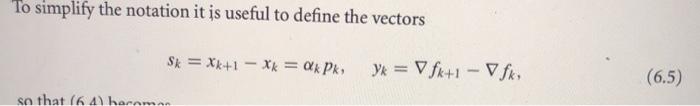
6.11 Use the properties of the trace of a symmetric matrix and the formula (6.19) to prove (6.44). trace(Bk+1) = trace(BK) || B S || 2 * + ST Bisk l|yx|l? yS (6.44) I (BFGS) Bk+1 k BeSxS BK s BS* + ! y sa (6.19) To simplify the notation it is useful to define the vectors Sk = Xk+1 - xk = ax Pk Yx = V fx+1-Vf (6.5) so that (64) harman Algorithm 6.1 (BFGS Method). Given starting point xo, convergence tolerance > 0, inverse Hessian approximation H.; k+ 0; while || fall > ; Compute search direction Pk = -HV fk; Set Xk+1 = xk + ax pk where ak is computed from a line search procedure to satisfy the Wolfe conditions (3.6); Define sk = Xk+1 xk and yk = Vfx+1 - Vfk; Compute Hx+1 by means of (6.17); kk + 1; end (while)