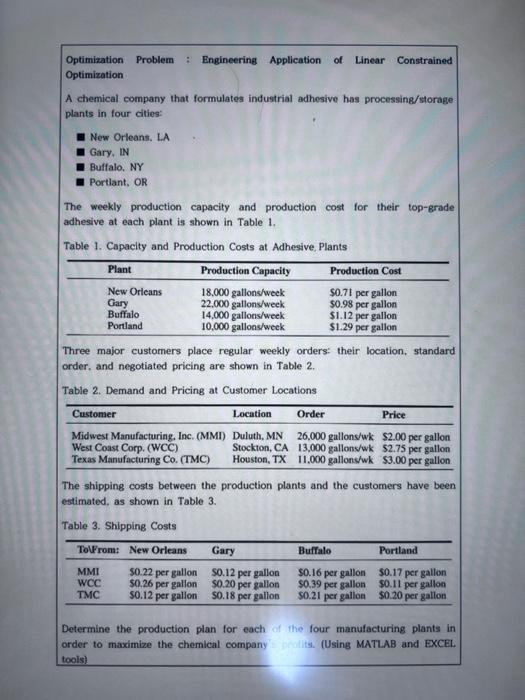
Optimization Problem Engineering Application of Linear Constrained Optimization A chemical company that formulates industrial adhesive has processing/storage plants in four cities: New Orleans, LA Gary, IN Buffalo, NY Portlant, OR The weekly production capacity and production cost for their top-grade adhesive at each plant is shown in Table 1. Table 1. Capacity and Production Costs at Adhesive, Plants Plant Production Capacity Production Cost New Orleans 18.000 gallons/week $0.71 per gallon Gary 22.000 gallons/week $0.98 per gallon Buffalo 14.000 gallons/week $1.12 per gallon Portland 10,000 gallons/weck $1.29 per gallon Three major customers place regular weekly orders: their location, standard order, and negotiated pricing are shown in Table 2. Table 2. Demand and Pricing at Customer Locations Customer Location Order Price Midwest Manufacturing, Inc. (MMI) Duluth, MN 26,000 gallo wk $2.00 per gallon West Coast Corp. (WCC) Stockton, CA 13,000 gallons/wk $2.75 per gallon Texas Manufacturing Co. (TMC) Houston, TX 11.000 gallons/wk $3.00 per gallon The shipping costs between the production plants and the customers have been estimated, as shown in Table 3. Table 3. Shipping Costs To\From: New Orleans Gary Buffalo Portland MMI WCC TMC 50.22 per gallon S0.12 per gallon 50.26 per gallon $0.20 per gallon $0.12 per gallon S0.18 per gallon $0.16 per gallon $0.17 per gallon 50.39 per gallon 50.11 per gallon $0.21 per gallon $0.20 per gallon Determine the production plan for each of the four manufacturing plants in order to maximize the chemical company realitet. (Using MATLAB and EXCEL tools) One of the primary functions of engineers is the design of new devices. processes, and systems. Engineering design can be defined as: "the process of applying scientific and mathematical principles for the purpose of defining a device. process or system that meets a given set of performance specifications and is optimal in some respect." This idea that the engineer is aiming for an optimal solution is important: the engineer is seeking not only a solution to the design problem. but is seeking a solution that is the best solution by some objective measure. The criterion that an engineer uses to determine which solution to a design problem is "best" may be vary from problem to problem, and even from engineer to engineer. In different cases, the best solutions may be the one that is least expensive, or more reliable, or lightest in weight, or smallest in size: it may be some other criterion, or even a combination of many fo theses criteria. Optimization is the mathematical process of determining the maximum or minimum value that a mathematical functions can take, and the values of the independent variables that yield these maximum or minimum values. In this project, we will examine both the formulation of optimization problems and the application of prewritten tools in MATLAB and EXCEL for the computational solution of optimization problems To develop an optimization problem in standard form - Step 1 : Identify the independent variables that must be assigned values. Step 2 : Identify the objective function, or the quantity that will be minimized or maximized in the optimization. Step 3: Identify any restrictions on the independent (design) variables and write these as equality or inequality equations. To solve optimization problems in MATLAB using pre-defined functions (The standard MATLAB function toolbox contains two optimal functions) - fminsearch: for performing nonlinear unconstrained multivariable optimization - fminbnd: for solving a particular type of nonlinear constrained optimization problems containing a single design variable Note that MATLAB also has an Optimization Toolbox available that contains a variety of more powerful tools used to solve a wider class of optimization problems. To solve optimization problems in EXCEL using the Solver tool. One of the primary functions of engineers is the design of new devices. processes, and systems. Engineering design can be defined as: "the process of applying scientific and mathematical principles for the purpose of defining a device. process or system that meets a given set of performance specifications and is optimal in some respect." This idea that the engineer is aiming for an optimal solution is important: the engineer is seeking not only a solution to the design problem. but is seeking a solution that is the best solution by some objective measure. The criterion that an engineer uses to determine which solution to a design problem is "best" may be vary from problem to problem, and even from engineer to engineer. In different cases, the best solutions may be the one that is least expensive, or more reliable, or lightest in weight, or smallest in size: it may be some other criterion, or even a combination of many fo theses criteria. Optimization is the mathematical process of determining the maximum or minimum value that a mathematical functions can take, and the values of the independent variables that yield these maximum or minimum values. In this project, we will examine both the formulation of optimization problems and the application of prewritten tools in MATLAB and EXCEL for the computational solution of optimization problems To develop an optimization problem in standard form - Step 1 : Identify the independent variables that must be assigned values. Step 2 : Identify the objective function, or the quantity that will be minimized or maximized in the optimization. Step 3: Identify any restrictions on the independent (design) variables and write these as equality or inequality equations. To solve optimization problems in MATLAB using pre-defined functions (The standard MATLAB function toolbox contains two optimal functions) - fminsearch: for performing nonlinear unconstrained multivariable optimization - fminbnd: for solving a particular type of nonlinear constrained optimization problems containing a single design variable Note that MATLAB also has an Optimization Toolbox available that contains a variety of more powerful tools used to solve a wider class of optimization problems. To solve optimization problems in EXCEL using the Solver tool. Optimization Problem : Engineering Application of Linear Constrained Optimization A chemical company that formulates industrial adhesive has processing/storage plants in four cities: New Orleans, LA Gary. IN Buffalo, NY Portlant, OR The weekly production capacity and production cost for their top-grade adhesive at each plant is shown in Table 1. Table 1. Capacity and Production Costs at Adhesive Plants Plant Production Capacity Production Cost New Orleans 18,000 gallons/week S0.71 per gallon Gary 22.000 gallons/weck $0.98 per gallon Buffalo 14,000 gallons/week $1.12 per gallon Portland 10.000 gallons/week $1.29 per gallon Three major customers place regular weekly orders: their location, standard order, and negotiated pricing are shown in Table 2. Table 2. Demand and Pricing at Customer Locations Customer Location Order Price Midwest Manufacturing, Inc. (MMI) Duluth, MN 26,000 gallons/wk $2.00 per gallon West Coast Corp. (WCC) Stockton, CA 13,000 gallons/wk $2.75 per gallon Texas Manufacturing Co. (TMC) Houston, TX 11.000 gallons/wk $3.00 per gallon The shipping costs between the production plants and the customers have been estimated, as shown in Table 3. Table 3. Shipping Costs To\From: New Orleans Gary Buffalo Portland MMI WCC TMC $0.22 per gallon 50.26 per gallon $0.12 per gallon 50.12 per gallon 50.20 per gallon $0.18 per gallon $0.16 per gallon $0.17 per gallon S0.39 per gallon $0.11 per gallon 50.21 per gallon 50.20 per gallon Determine the production plan for each of the four manufacturing plants in order to maximize the chemical company calits (Using MATLAB and EXCEL tools) Optimization Problem Engineering Application of Linear Constrained Optimization A chemical company that formulates industrial adhesive has processing/storage plants in four cities: New Orleans, LA Gary, IN Buffalo, NY Portlant, OR The weekly production capacity and production cost for their top-grade adhesive at each plant is shown in Table 1. Table 1. Capacity and Production Costs at Adhesive, Plants Plant Production Capacity Production Cost New Orleans 18.000 gallons/week $0.71 per gallon Gary 22.000 gallons/week $0.98 per gallon Buffalo 14.000 gallons/week $1.12 per gallon Portland 10,000 gallons/weck $1.29 per gallon Three major customers place regular weekly orders: their location, standard order, and negotiated pricing are shown in Table 2. Table 2. Demand and Pricing at Customer Locations Customer Location Order Price Midwest Manufacturing, Inc. (MMI) Duluth, MN 26,000 gallo wk $2.00 per gallon West Coast Corp. (WCC) Stockton, CA 13,000 gallons/wk $2.75 per gallon Texas Manufacturing Co. (TMC) Houston, TX 11.000 gallons/wk $3.00 per gallon The shipping costs between the production plants and the customers have been estimated, as shown in Table 3. Table 3. Shipping Costs To\From: New Orleans Gary Buffalo Portland MMI WCC TMC 50.22 per gallon S0.12 per gallon 50.26 per gallon $0.20 per gallon $0.12 per gallon S0.18 per gallon $0.16 per gallon $0.17 per gallon 50.39 per gallon 50.11 per gallon $0.21 per gallon $0.20 per gallon Determine the production plan for each of the four manufacturing plants in order to maximize the chemical company realitet. (Using MATLAB and EXCEL tools) One of the primary functions of engineers is the design of new devices. processes, and systems. Engineering design can be defined as: "the process of applying scientific and mathematical principles for the purpose of defining a device. process or system that meets a given set of performance specifications and is optimal in some respect." This idea that the engineer is aiming for an optimal solution is important: the engineer is seeking not only a solution to the design problem. but is seeking a solution that is the best solution by some objective measure. The criterion that an engineer uses to determine which solution to a design problem is "best" may be vary from problem to problem, and even from engineer to engineer. In different cases, the best solutions may be the one that is least expensive, or more reliable, or lightest in weight, or smallest in size: it may be some other criterion, or even a combination of many fo theses criteria. Optimization is the mathematical process of determining the maximum or minimum value that a mathematical functions can take, and the values of the independent variables that yield these maximum or minimum values. In this project, we will examine both the formulation of optimization problems and the application of prewritten tools in MATLAB and EXCEL for the computational solution of optimization problems To develop an optimization problem in standard form - Step 1 : Identify the independent variables that must be assigned values. Step 2 : Identify the objective function, or the quantity that will be minimized or maximized in the optimization. Step 3: Identify any restrictions on the independent (design) variables and write these as equality or inequality equations. To solve optimization problems in MATLAB using pre-defined functions (The standard MATLAB function toolbox contains two optimal functions) - fminsearch: for performing nonlinear unconstrained multivariable optimization - fminbnd: for solving a particular type of nonlinear constrained optimization problems containing a single design variable Note that MATLAB also has an Optimization Toolbox available that contains a variety of more powerful tools used to solve a wider class of optimization problems. To solve optimization problems in EXCEL using the Solver tool. One of the primary functions of engineers is the design of new devices. processes, and systems. Engineering design can be defined as: "the process of applying scientific and mathematical principles for the purpose of defining a device. process or system that meets a given set of performance specifications and is optimal in some respect." This idea that the engineer is aiming for an optimal solution is important: the engineer is seeking not only a solution to the design problem. but is seeking a solution that is the best solution by some objective measure. The criterion that an engineer uses to determine which solution to a design problem is "best" may be vary from problem to problem, and even from engineer to engineer. In different cases, the best solutions may be the one that is least expensive, or more reliable, or lightest in weight, or smallest in size: it may be some other criterion, or even a combination of many fo theses criteria. Optimization is the mathematical process of determining the maximum or minimum value that a mathematical functions can take, and the values of the independent variables that yield these maximum or minimum values. In this project, we will examine both the formulation of optimization problems and the application of prewritten tools in MATLAB and EXCEL for the computational solution of optimization problems To develop an optimization problem in standard form - Step 1 : Identify the independent variables that must be assigned values. Step 2 : Identify the objective function, or the quantity that will be minimized or maximized in the optimization. Step 3: Identify any restrictions on the independent (design) variables and write these as equality or inequality equations. To solve optimization problems in MATLAB using pre-defined functions (The standard MATLAB function toolbox contains two optimal functions) - fminsearch: for performing nonlinear unconstrained multivariable optimization - fminbnd: for solving a particular type of nonlinear constrained optimization problems containing a single design variable Note that MATLAB also has an Optimization Toolbox available that contains a variety of more powerful tools used to solve a wider class of optimization problems. To solve optimization problems in EXCEL using the Solver tool. Optimization Problem : Engineering Application of Linear Constrained Optimization A chemical company that formulates industrial adhesive has processing/storage plants in four cities: New Orleans, LA Gary. IN Buffalo, NY Portlant, OR The weekly production capacity and production cost for their top-grade adhesive at each plant is shown in Table 1. Table 1. Capacity and Production Costs at Adhesive Plants Plant Production Capacity Production Cost New Orleans 18,000 gallons/week S0.71 per gallon Gary 22.000 gallons/weck $0.98 per gallon Buffalo 14,000 gallons/week $1.12 per gallon Portland 10.000 gallons/week $1.29 per gallon Three major customers place regular weekly orders: their location, standard order, and negotiated pricing are shown in Table 2. Table 2. Demand and Pricing at Customer Locations Customer Location Order Price Midwest Manufacturing, Inc. (MMI) Duluth, MN 26,000 gallons/wk $2.00 per gallon West Coast Corp. (WCC) Stockton, CA 13,000 gallons/wk $2.75 per gallon Texas Manufacturing Co. (TMC) Houston, TX 11.000 gallons/wk $3.00 per gallon The shipping costs between the production plants and the customers have been estimated, as shown in Table 3. Table 3. Shipping Costs To\From: New Orleans Gary Buffalo Portland MMI WCC TMC $0.22 per gallon 50.26 per gallon $0.12 per gallon 50.12 per gallon 50.20 per gallon $0.18 per gallon $0.16 per gallon $0.17 per gallon S0.39 per gallon $0.11 per gallon 50.21 per gallon 50.20 per gallon Determine the production plan for each of the four manufacturing plants in order to maximize the chemical company calits (Using MATLAB and EXCEL tools)