Options & volatility analysis

Options & volatility analysis Refer to supplement which contains data on call option prices and implied volatilities on the Nasdaq 100 index. The spot reference rate for all prices is 14940. Each individual option contract is written on 100 shares of stock, at a set strike price, for a given expiration date. These are European-style options which can only be exercised at expiry.

A delta (DM) of 0.50 implies that for a 1% rise in the spot rate,the price of the call option is expected to rise by 0.50%. A delta of -0.50 implies that for a 1% rise in the spot rate, the price of the put option is expected to fall by 0.50%. Implied volatility (IVM), very much like interest rate yield, is always quoted in annualized percentage terms. A reading of 15.00 (i.e. 15%) is equivalent to a 1 standard deviation move on the underlying spot rate over a 1-year period. For interpreting implied volatility or expected standard deviation for a nominal 1-month period, however, the implied volatility must be de-annualized as follows IVd=IV M?112. Similarly, For interpreting implied volatility or expected standard deviation for a nominal 6-month period, however, the implied volatility must be de-annualized as follows IVd=IV M?612, and so on.

Problem set supplement

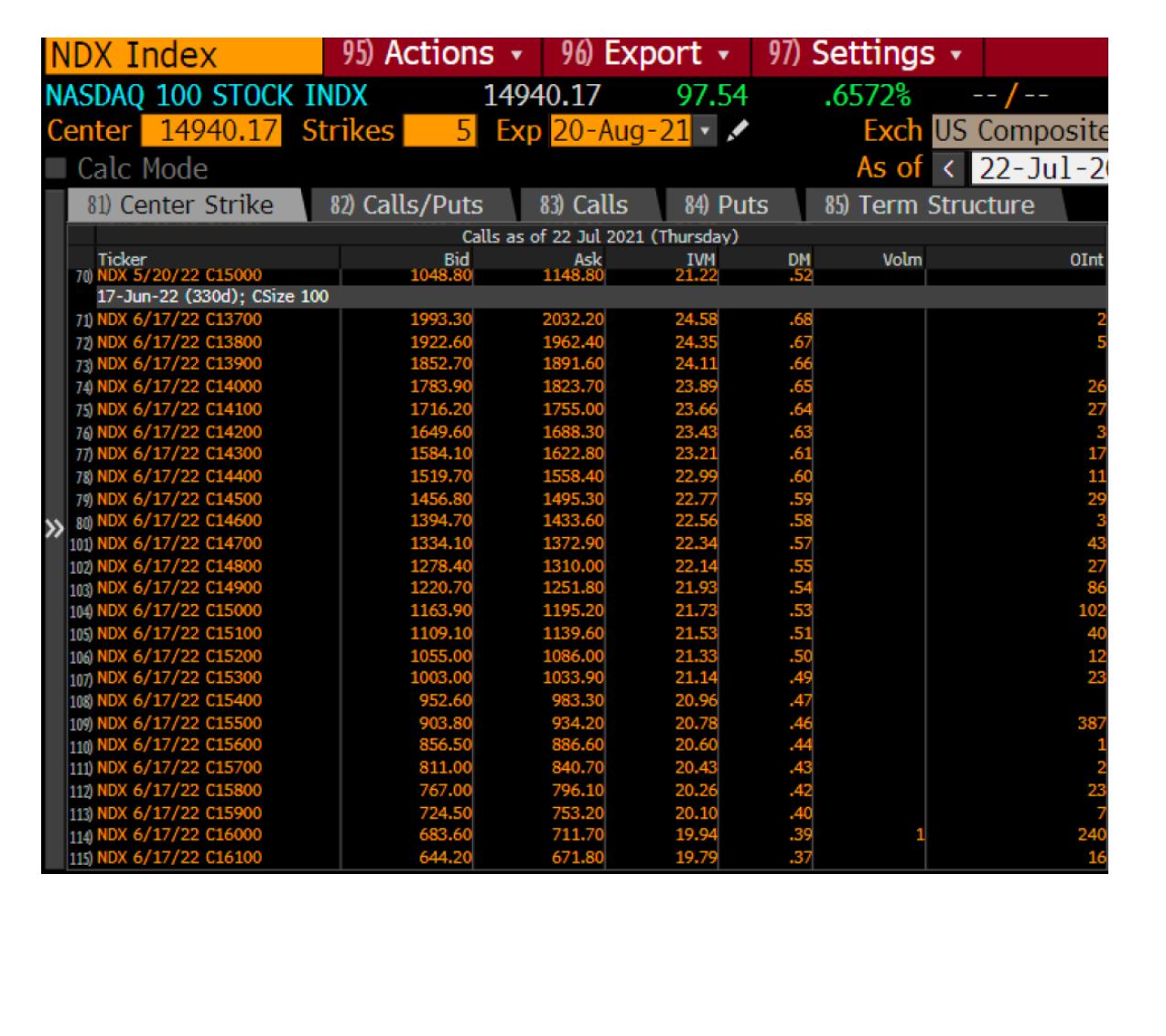
Call option prices below are written on NASDAQ 100 index as of Jul-22-2021 for two separate expiry dates, Aug-20-2021 and Jun-17-2022

Spot was 14940 when the prices the prices were generated.

Please Refer the attachments below as reference to solve the questions:

Questions on basics and definitions:

5. If the index falls by 1% immediately after the option is purchased, what is the approximate new price of the August expiry C15000 call option? Use delta to approximate the new price.

6. Use the Black-Scholes model provided to find exact answer for previous question.

7. If the index rises by 1% immediately after the option is purchased, what is the approximate new price of the June expiry C15000 call option? Use delta to approximate the new price.

8. Use the Black-Scholes model provided to find exact answer for previous question.

9. Vega is the rate of change of the option price subject to changes in implied volatility. In other words, it is the first derivative of the price with respect to changes in implied volatility. Produce a graph with the delta of an option on the x-axis and vega on the y-axis. What is the intuition behind how vega changes with delta?

10. Which June expiry call contract in the supplement has the highest vega?

11. Which August expiry contract in the supplement has the lowest vega?

12. How does implied volatility change with tenor for Nasdaq100 options? This is known as term structure. What is the intuition behind this?

NDX Index 95) Actions . 96) Export . 97) Settings . NASDAQ 100 STOCK INDX 14940.17 97.54 6572% Center 14940.17 Strikes 5 Exp 20-Aug-21 Exch US Composite Calc Mode As of