Ordinary Differential Equations Section 5.1 Homework Problem #1

Considering the 1st order linearly homogeneous system of equations below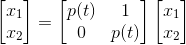

The system of equations above is not a constant coefficient but has a fundamental matrix of solutions "x(t)" that can be represented by quadrature Find such a matrix x(t) then compute its special version that manages it to be known as the identity matrix when at t=0. We know that since this 1st order linearly homogeneous system of equations isn't a constant coefficient the laplace transform won't work so remember that when looking at a fundamental matrix of solutions x(t) one wants that

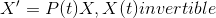which is equal to 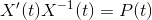as well as for a special fundamental matrix you want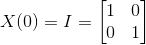

Please show all of your work thanks!

01 1 T1 p(t) 0 12 plt) 22 X' = P(t)X, X(t)invertible X'(t)x-1(t) = P(t) X(0) = 1 = 1 0 0 1 01 1 T1 p(t) 0 12 plt) 22 X' = P(t)X, X(t)invertible X'(t)x-1(t) = P(t) X(0) = 1 = 1 0 0 1