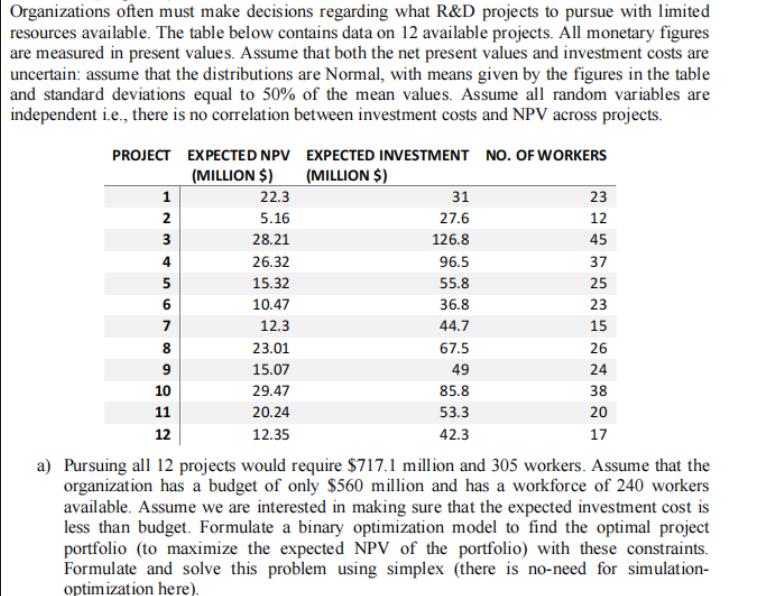
Organizations often must make decisions regarding what R&D projects to pursue with limited resources available. The table below contains data on 12 available projects. All monetary figures are measured in present values. Assume that both the net present values and investment costs are uncertain: assume that the distributions are Normal, with means given by the figures in the table and standard deviations equal to 50% of the mean values. Assume all random variables are independent i.e., there is no correlation between investment costs and NPV across projects. PROJECT EXPECTED NPV EXPECTED INVESTMENT NO. OF WORKERS 1 (MILLION $) 22.3 (MILLION $) 31 23 2 5.16 27.6 12 3 28.21 126.8 45 4 26.32 96.5 37 5 15.32 55.8 25 6 10.47 36.8 23 7 12.3 44.7 15 8 23.01 67.5 26 9 15.07 49 24 10 29.47 85.8 38 11 20.24 53.3 20 12 12.35 42.3 17 a) Pursuing all 12 projects would require $717.1 million and 305 workers. Assume that the organization has a budget of only $560 million and has a workforce of 240 workers available. Assume we are interested in making sure that the expected investment cost is less than budget. Formulate a binary optimization model to find the optimal project portfolio (to maximize the expected NPV of the portfolio) with these constraints. Formulate and solve this problem using simplex (there is no-need for simulation- optimization here). b) Using the answer obtained in part a) simulate the true NPV and Cost of the portfolio (there is no need for a mathematical formulation). What is the probability that the true cost exceeds the budget? Run the simulation with 20.000 iterations. c) Requiring that the mean expected cost to be lower than the budget can be problematic as roughly 50% of the time we will be exceeding budget. Instead, you are interested in a portfolio budget whose probability of exceeding the budget is at most 20%. What is optimal portfolio. There is no need for a math formulation. Hint: use simulation- optimization with 1000 iterations and 50 trials in the interest of speed. d)(Bonus Question 20 points) Suggest an approach that allows you to answer part c) using GRG Non-linear. Hint: using the fact that costs are independent, can you write down an excel formula (without using @Risk) for the probability of exceeding the budget to add as a constraint in excel solver? Note that GRG Nonlinear can handle constraints of the form "Probability(some random variable >target value) some number", as long as you can specify the right parameters of the probability distribution.