P#2. The Newton Method.

Write code to find one root of the function x^5 100 = 0 using the popular Newton method. By this method:

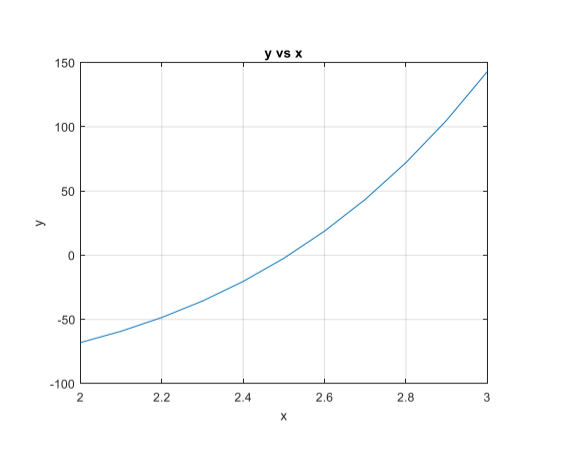
(1) Graph the function you want the root for. The graph must show one of the roots. (2) Select the root you are interested in and zoom the graph around this point. (3) Select a point close to the root (e.g. x0 = 2.6 ) (4) Feed x0 into the Newtons recurrence formula to find a new approximation to the root xn. The new approximation xn should be closer to the root than x0 for the method to converge.

The Newtons recurrence formula:

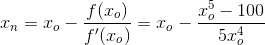
(5) Before the next iteration, xn becomes the new initial point x0 and the process starts over again (4). (6) Stops the iterative process when you reach an error less 1x10^-5; error is defined as

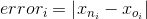
Submit plot code, function plot (output), Newtons method code, and output (the found root):

% LearningToPlot % Plots f(x)=x^5-100 % x [axis], y [axis]

clc, clear, clf

% Create two vectors x=1:0.1:3.0; y=x.^5-100;

% Plot the function plot(x,y); grid on xlim([2.0 3.0]); % limits the x-range xlabel('x'); ylabel ('y'); title('y vs x');

(I need this in Matlab code, thank you)