Packet bed mass transfer

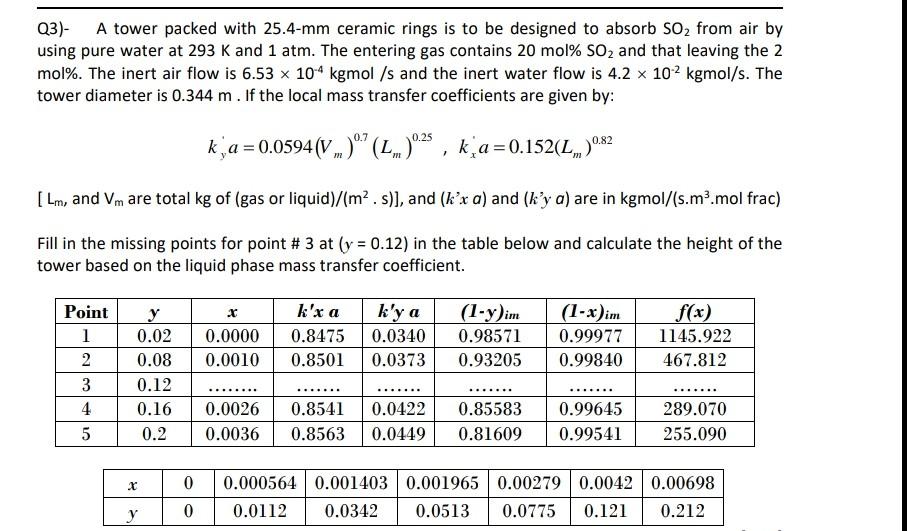
Q3)- A tower packed with 25.4-mm ceramic rings is to be designed to absorb SO2 from air by using pure water at 293 K and 1 atm. The entering gas contains 20 mol% SO2 and that leaving the 2 mol%. The inert air flow is 6.53 x 104 kgmol /s and the inert water flow is 4.2 x 102 kgmol/s. The tower diameter is 0.344 m. If the local mass transfer coefficients are given by: 0.25 k a = 0.0594 (V.)"" (...)"25, ka=0.152(L.).82 [Lm, and Vm are total kg of (gas or liquid)/(m2.s)), and (kx a) and (ky a) are in kgmol/(s.m.mol frac) Fill in the missing points for point # 3 at (y = 0.12) in the table below and calculate the height of the tower based on the liquid phase mass transfer coefficient. x Point 1 2 3 4 0.0000 0.0010 k'x a 0.8475 0.8501 k'ya 0.0340 0.0373 (1-y)im 0.98571 0.93205 (1-x)im 0.99977 0.99840 f(x) 1145.922 467.812 0.02 0.08 0.12 0.16 0.2 ..... ...... ....... 0.0026 0.0036 0.8541 0.8563 0.0422 0.0449 0.85583 0.81609 0.99645 0.99541 289.070 255.090 5 0 0 0.000564 0.001403 0.001965 0.00279 0.0042 0.00698 0.0112 0.0342 0.0513 0.0775 0.121 0.212 The height of the packed column based on the overall mass transfer coefficient is given by: Z=Hoy * Nov For dilute mixtures: out Nov Vam - Youwhere (yn-yi) = - (7.-9.)..-(y.-yild , (y:- y.) [(y1 - y.). [(y - y. Dom ] mV Hoy = H, + In H L Numerical integration using Trapezoidal rule is given by: $*fcwdx = (6-4) f(a) +86) = a fa+ f(b 2