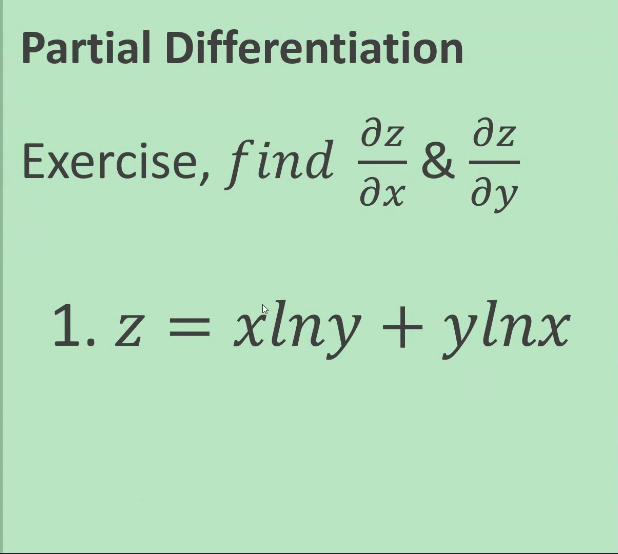
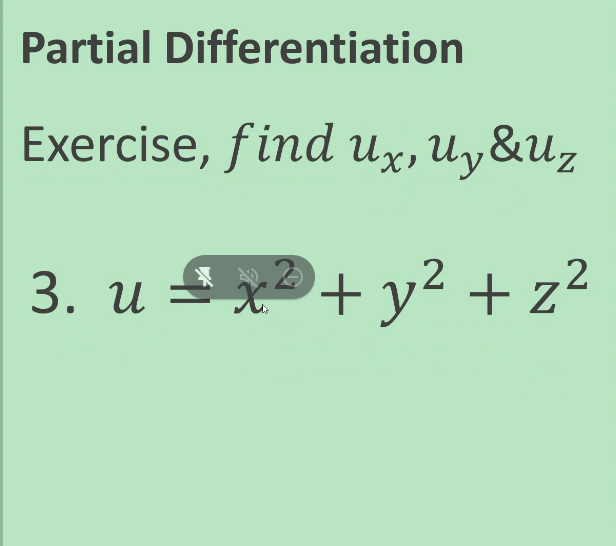
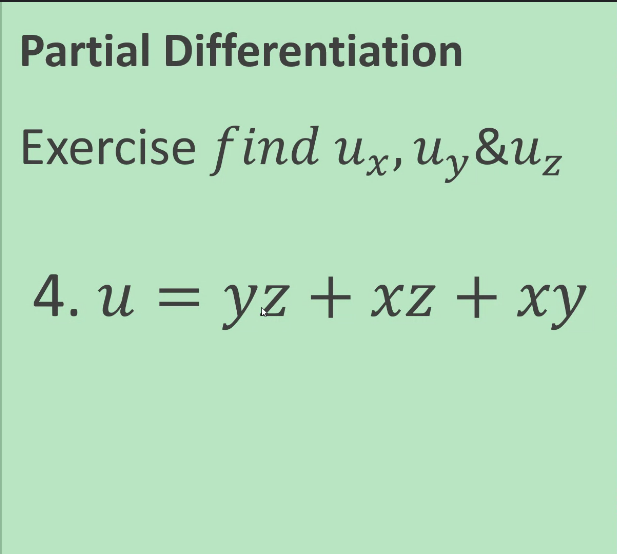
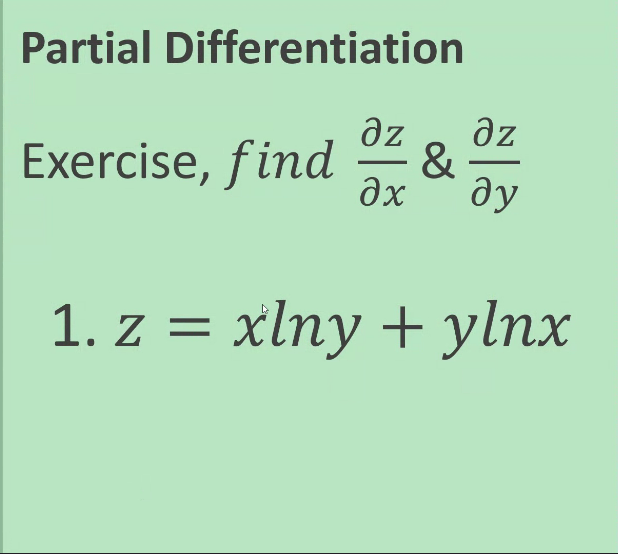
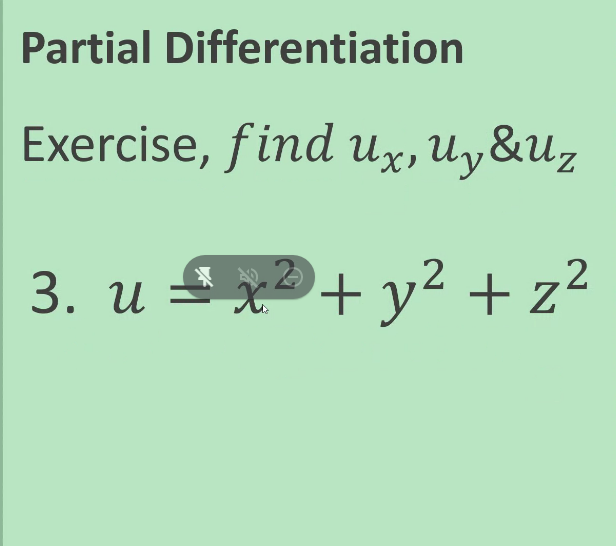
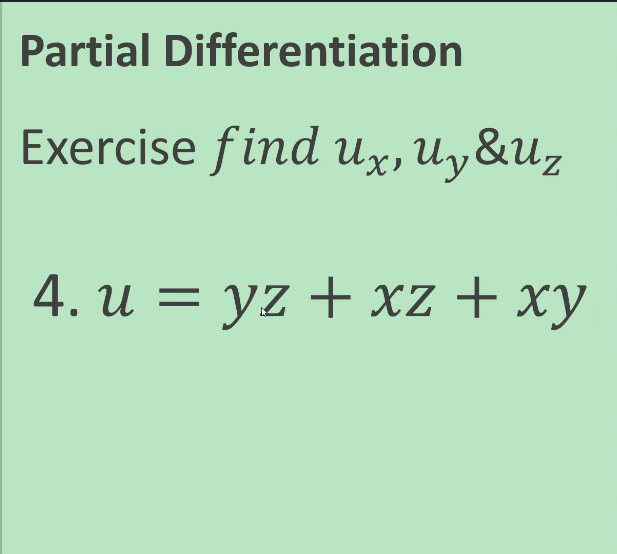
PARAMETRIC EQUATIONS Find - and day and simplify whenever possible dx dx2 Exercise 1 x = + +1,y = +2 + 1 Exercise 2 x - cose + Osine, y - sine - Acose Exercise 3 x = 1-Int,y = t - IntPARAMETRIC EQUATIONS 7.3 Radius of Curvature Find the radius of curvature at the given point: Exercises 1. x = tz - 2t, y = 1 - 4tatt = 1. Exercises 2. y = "( eate a ) at (0,a) 72+4 at (2,0) Exercises 3. X = 2+4Partial Differentiation Oz Oz Exercise, find & Ox ay 1. z = xlny + ylnxPartial Differentiation az Oz Exercise, find & ax ay y 2. z = xyArctanPartial Differentiation Exercise, find ux, Uy &Uz 3. u * + V 2 yz+ ZPartial Differentiation Exercise find ux, Uy &Uz 4. u = yz + xz + xyPartial Differentiation Partial Derivative of Higher Order Exercise. Find azz azz & azz ax2' ayox dy2 1. z = 3x2y3 - 4x4y2Partial Differentiation Partial Derivative of Higher Order a2 z Exercise. Find azz azz & ax2 ' ayax dy2 2. z = x2 siny + y?cosxPartial Differentiation Partial Derivative of Higher Order azz azz azz Exercise. Find & ax2 ' ayox dy2 3. z = (x+ y) 3