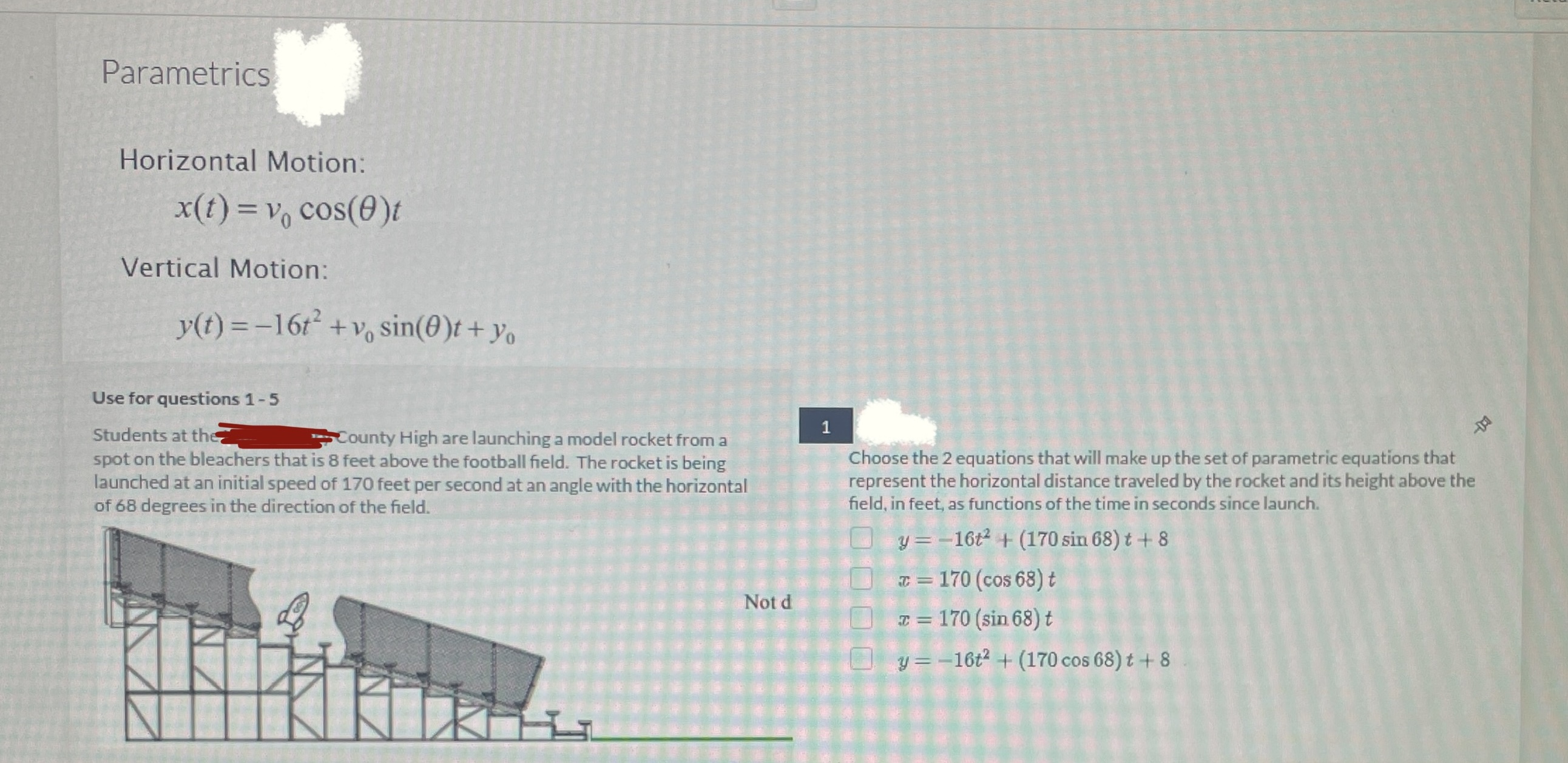
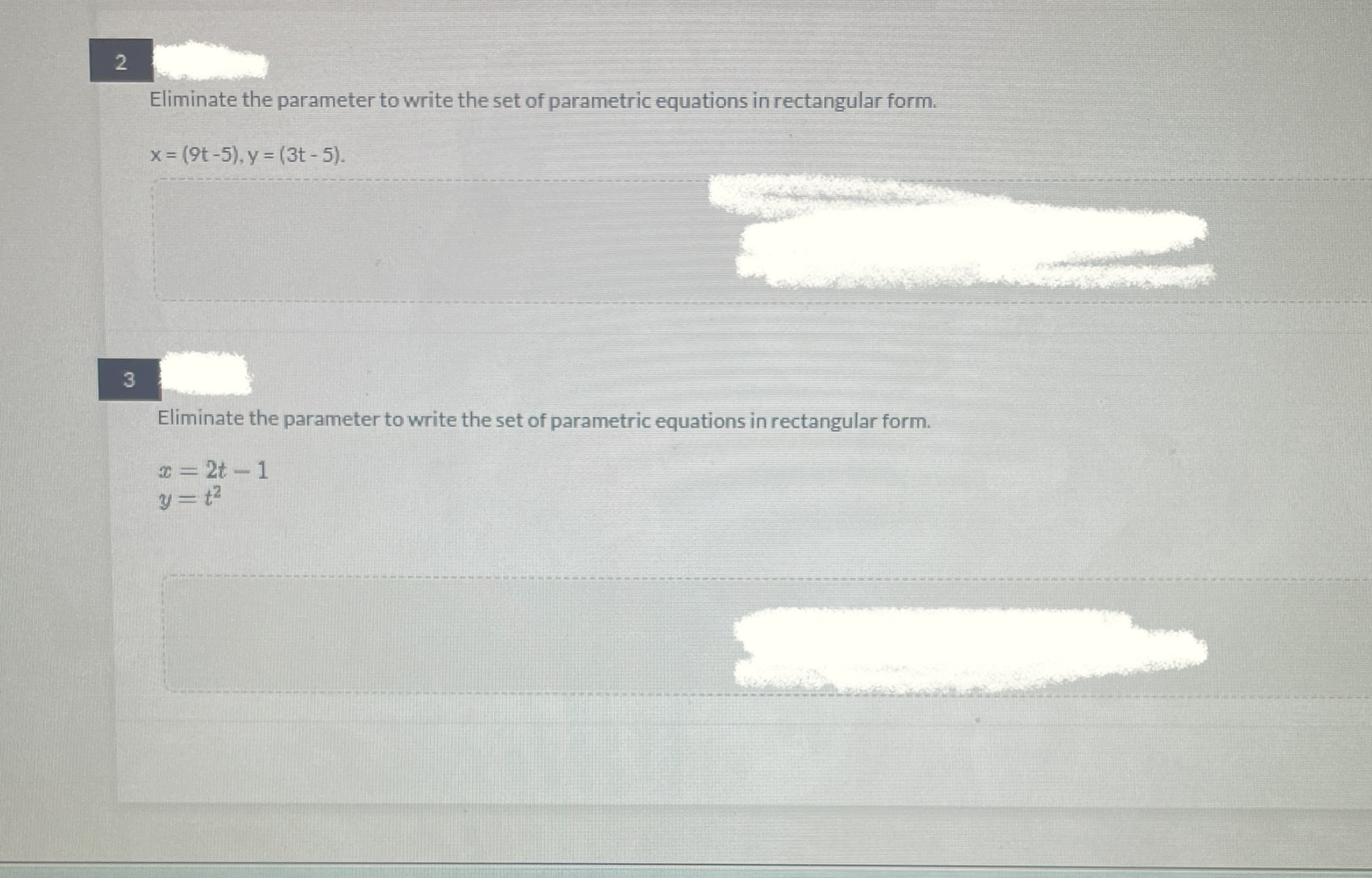
Parametrics Horizontal Motion: x(t) = v cos(0)t Vertical Motion: y(t)=-16t+v, sin(0)t + yo Use for questions 1-5 Students at the County High are launching a model rocket from a spot on the bleachers that is 8 feet above the football field. The rocket is being launched at an initial speed of 170 feet per second at an angle with the horizontal of 68 degrees in the direction of the field. Not d Choose the 2 equations that will make up the set of parametric equations that represent the horizontal distance traveled by the rocket and its height above the field, in feet, as functions of the time in seconds since launch. y=-16t + (170 sin 68) t + 8 x = 170 (cos 68) t z=170 (sin 68) t y=-16t2 + (170 cos 68) t + 8 - 2 Eliminate the parameter to write the set of parametric equations in rectangular form. x=(9t-5), y = (3-5). 3 Eliminate the parameter to write the set of parametric equations in rectangular form. x=2t-1 y=t