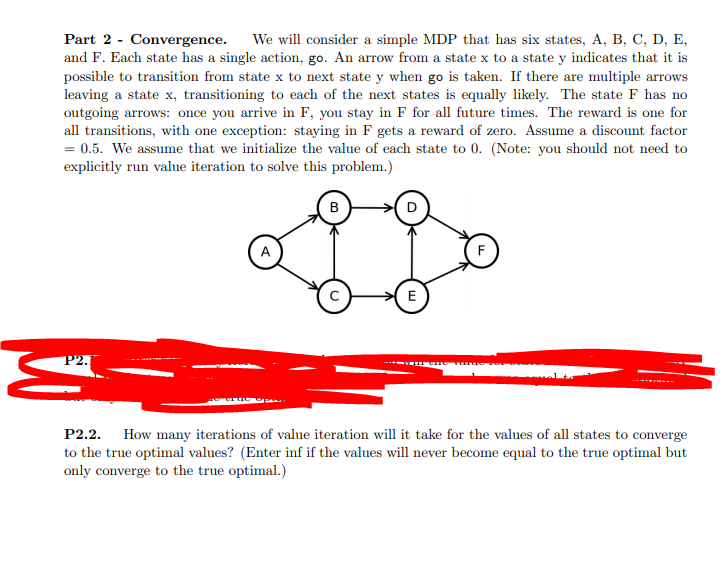
Part 2 - Convergence. We will consider a simple MDP that has six states, A, B, C, D, E, and F. Each state has a single action, go. An arrow from a state x to a state y indicates that it is possible to transition from state x to next state y when go is taken. If there are multiple arrows leaving a state x, transitioning to each of the next states is equally likely. The state F has no outgoing arrows: once you arrive in F, you stay in F for all future times. The reward is one for all transitions, with one exception: staying in F gets a reward of zero. Assume a discount factor = 0.5. We assume that we initialize the value of each state to 0. (Note: you should not need to explicitly run value iteration to solve this problem.) E P2.2. How many iterations of value iteration will it take for the values of all states to converge to the true optimal values? (Enter inf if the values will never become equal to the true optimal but only converge to the true optimal.)