Question: Part 2: Function Notation and Compositions A. f = {(-2, 3), (-1, 1), (0, 0), (1, -1), (2, -3)} g = {(-3, 1), (-1, -2),

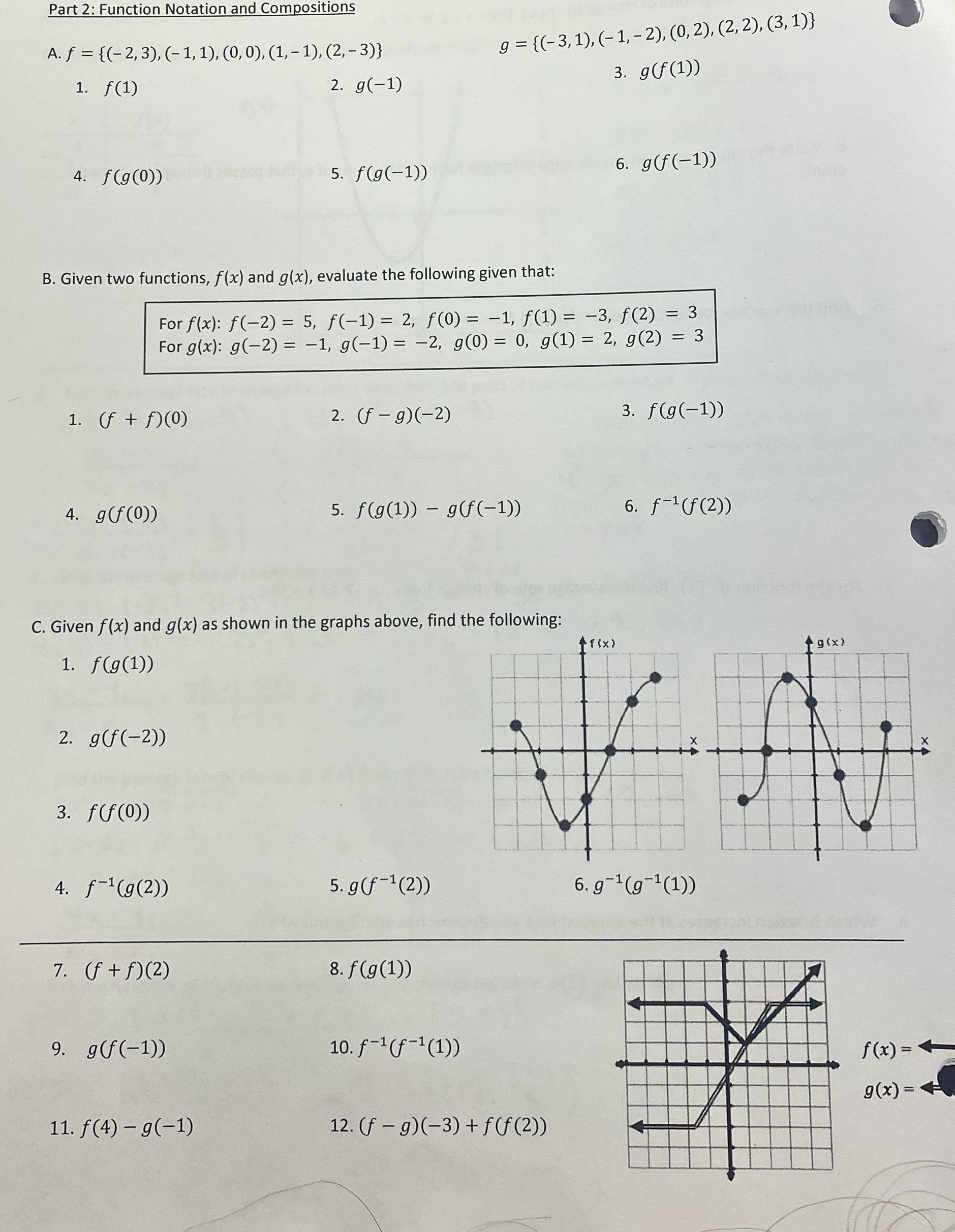
Part 2: Function Notation and Compositions A. f = {(-2, 3), (-1, 1), (0, 0), (1, -1), (2, -3)} g = {(-3, 1), (-1, -2), (0, 2), (2, 2), (3, 1)} 1. f(1) 2. g(-1) 3. g(f (1)) 4. f(g(0)) 5. f(g(-1) ) 6. g(f(-1)) B. Given two functions, f(x) and g(x), evaluate the following given that: For f (x): f ( - 2) = 5, f (- 1) = 2, f(0) = -1, f(1) = -3, f(2) = 3 For g(x): g(-2) = -1, g(-1) = -2, g(0) = 0, g(1) = 2, g(2) = 3 1 . ( f + f ) (0 ) 2. (f - 9) (-2) 3. f(g(-1)) 4. g(f(0)) 5 . f(g (1) ) - 9(f(-1)) 6. f-1 (f (2) ) C. Given f(x) and g(x) as shown in the graphs above, find the following: 19 ( x ) 1. f(g(1)) 2. gcf (-2) ) 3. f(f (0) ) 4. f-1(9 (2) ) 5. g ( f -1 (2) ) 6.9-1(9-1(1)) 7. (f + f) (2) 8. f(g(1)) 9. g(f(-1) ) 10 . f-1 (f-1 (1) ) f (x) =+ 9 (x ) = 4 11. f(4) - g(-1) 12. (f - g) (- 3) + f(f (2 ) )

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Question 1. Given the project network and baseline information below, complete the form to develop a status report for the project at the end of period 4 and the end of period 8. From the data you...

Homework: Chapter ... Question 2, Problem 24 Part 2 of 2 HW Score: 0%, 0 of 3 points Points: 0 of 1 Save Smith Schroeder, and Tom (SST) is a short haul household furniture moving company SST's labor...

Please answer all 4 parts and label every step taken. 7 Consider the following two games, with ( > 0: Game 1: b1 b2 a1 1, 1, 1 0, 0, 0 a2 0, 0, 0 9, 9, 10 Game 2: b1 b2 a1 10, 10, F 10, 0, -1 a2 0,...

THQ 2 PS 1 Yoldeof Purchase Yield * 100 0 00 - 98306 190 = 0-03507 3.5 1% Sale Yield * 9 49000 - 98300 = 0 . 03512 = 3:51% The lower yield will came a higher p and bank bill price If Gearse -accepts...

The function fis given by the set {(-5, 3), (-1, -1), (0, 4), (2, -6), (5, -7)}.Determine f- The function fis given by the set {(-5, 3), (-1, -I), (O, 4), (2, -6), (5, -7)). Determine

Following questions regard ANOVA analysis Simultaneous Tests for General Linear Hypotheses Multiple Comparisons of Means: Tukey Contrasts Fit: aov (formula = gluten . percentage ~ company, data =...

Intro Estimated sales for the next four months are as follows (in 5 million). Month Cash sales Credit sales 1 47.08 94.16 2 50.38 75.56 3 53.9 80.85 4 57.68 86.51 The firm collects 50% of credit...

Intro Estimated sales for the next four months are as follows (in $ million): Month 1 2 3 4 Cash sales Credit sales 58.8 51.36 102.72 54.96 82.43 62.92 88.2 94.38 The firm collects 20% of credit...

Homework Unit 7 MATH 0307 14 1 2 solving systems by grap Solve the system of linear equations by graphing x y 1 x y 3 Use the graphing tool to graph the system AXED Select the correct choice below...

Draw a Venn Diagram to represent the following sets, and answer questions: The universal set: U = {-9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9} A = {-8, -6, -4, -2, 0, 2, 4, 6,...

Calculate and compare the market values of a $100,000 face value Government of Canada Treasury bill on dates that are 91 days, 61 days, 31 days, and one day before maturity. Assume that the rate of...

A single production line processes 6 different items with the data below. Determine the production quantities and order intervals for each of item. (0.4 points) A $300 20% 1 2 3 4 6 5,000 $15 15,000...

Coppinger Corp. is considering the use of a computer to assign probability distributions to the input variables used in the analysis. The computer would then randomly select input variables from...

On 1 March 2007 DB Limited issued R560 000 15% debentures at R98. The debentures were to be redeemed at par in four equal annual payments starting 28 February 2010. Required: Journalise the above...