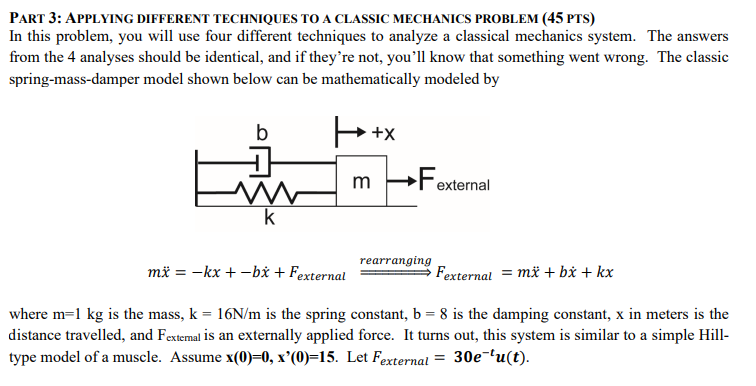
PART 3: APPLYING DIFFERENT TECHNIQUES TO A CLASSIC MECHANICS PROBLEM (45 PTS) In this problem, you will use four different techniques to analyze a classical mechanics system. The answers from the 4 analyses should be identical, and if they're not, you'll know that something went wrong. The classic spring-mass-damper model shown below can be mathematically modeled by + +x m F. external k rearranging mx = -kx + -bx + Fexternal Fexternal = mx + bx + kx where m=1 kg is the mass, k = 16N/m is the spring constant, b = 8 is the damping constant, x in meters is the distance travelled, and Fextemal is an externally applied force. It turns out, this system is similar to a simple Hill- type model of a muscle. Assume x(0)=0, x'(0)=15. Let Fexternal = 30e tu(t).2. Analyze the system using convolution. (12 pts) An alternative method to find the total system response is by using convolution. You've calculated convolutions before and now you'll be able to see where it can be useful. Recall, you'll want to convolve Fextemal with the system's impulse response, h(t). 1. First, you'll need to find the system's step response, which is the zero state response but with Fexternal set to a value of 1. 2. Given that the derivative of unit step is an impulse, you can now find the system's impulse response, h(t). In the upper right of a 2x2 subplot, plot the result of convolving Fexternal with the impulse response of the system. Don't forget to multiply your convolution solution by dt, which was the scaling technique you should have discovered during your convolution lab.Q2.1 What is the system's impulse response in terms of t? Q2.2 You should notice that the resulting plot does not achieve the same amplitude as the TSR in the first subplot. Recall, when you used dsolve() to find the step response, you were approaching the part of the problem that solves the zero state response. What do you need to add to your convolution solution to achieve the TSR? Now add a second line to the upper right of a 2x2 subplot with this adjustment. Remember: labels, units, legends, titles, and distinct lines