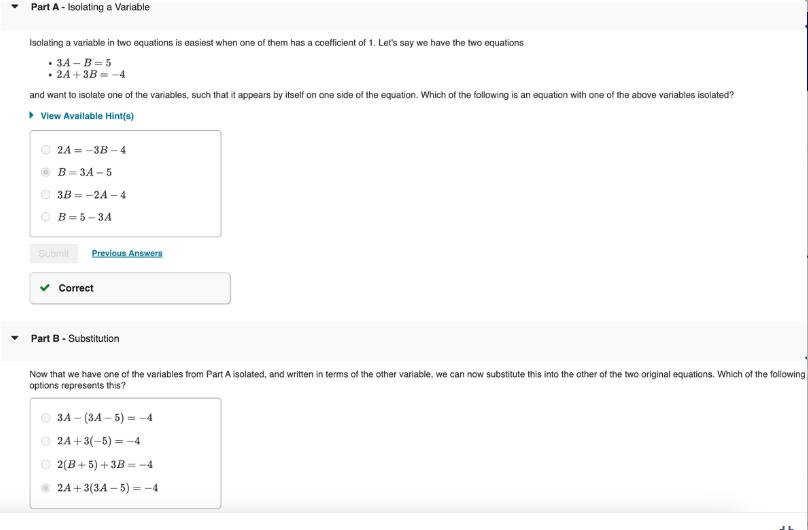
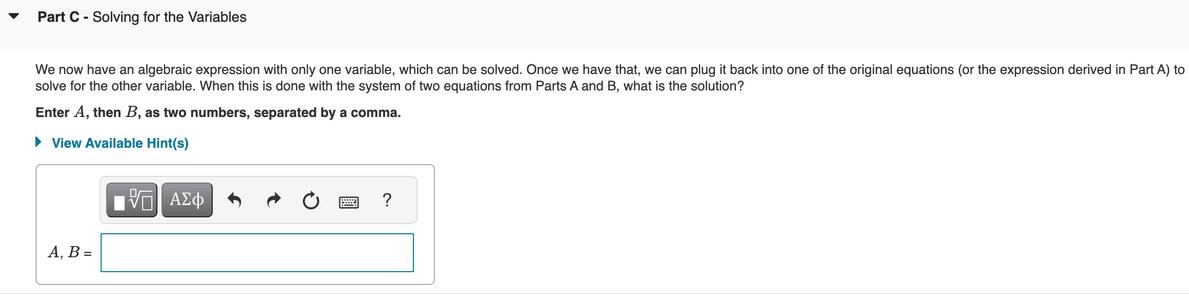
Part A - Isolating a Variable Isolating a variable in two equations is easiest when one of them has a coefficient of 1. Let's say we have the two equations . 3A-B=5 . 2A+3B=-4 and want to isolate one of the variables, such that it appears by itself on one side of the equation. Which of the following is an equation with one of the above variables isolated? View Available Hint(s) 2A -3B-4 B=3A-5 3B -2A-4 B=5-3A Submit Correct Previous Answers Part B - Substitution Now that we have one of the variables from Part A isolated, and written in terms of the other variable, we can now substitute this into the other of the two original equations. Which of the following options represents this? 3A (3A-5)=-4 2A+3(-5)=-4 2(B+5)+3B=-4 2A+3(3A-5)=-4 Part C - Solving for the Variables We now have an algebraic expression with only one variable, which can be solved. Once we have that, we can plug it back into one of the original equations (or the expression derived in Part A) to solve for the other variable. When this is done with the system of two equations from Parts A and B, what is the solution? Enter A, then B, as two numbers, separated by a comma. View Available Hint(s) A, B = ?