Part B $-$ Tutorial: Always find the support reaction before analyzing the truss. Using the method of sections to find the truss forces.

If a truss is in equilibrium then every member in the truss must also be in equilibrium. This principle is used in analyzing a truss using the method of sections. To apply the method of

sections, we use an imaginary cut through members of the truss to expose the forces in those members as external forces.

If the free$-$body diagram of the joint on either side of the cut is known, we can apply the equations of equilibrium to that part of the member to determine the forces at the cut section.

Since only three equilibrium equations $,$ and ${\displaystyle \underset{?}{\overset{?}{}}}{M}_O=0)$ can be applied to the free$-$body diagram of any segment, we should try to select a cut that passes

through no more than three members of the truss in which the forces are unknown. Note that the moment equation can be written multiple times, but there are still only $3$ independent

equilibrium equations available.

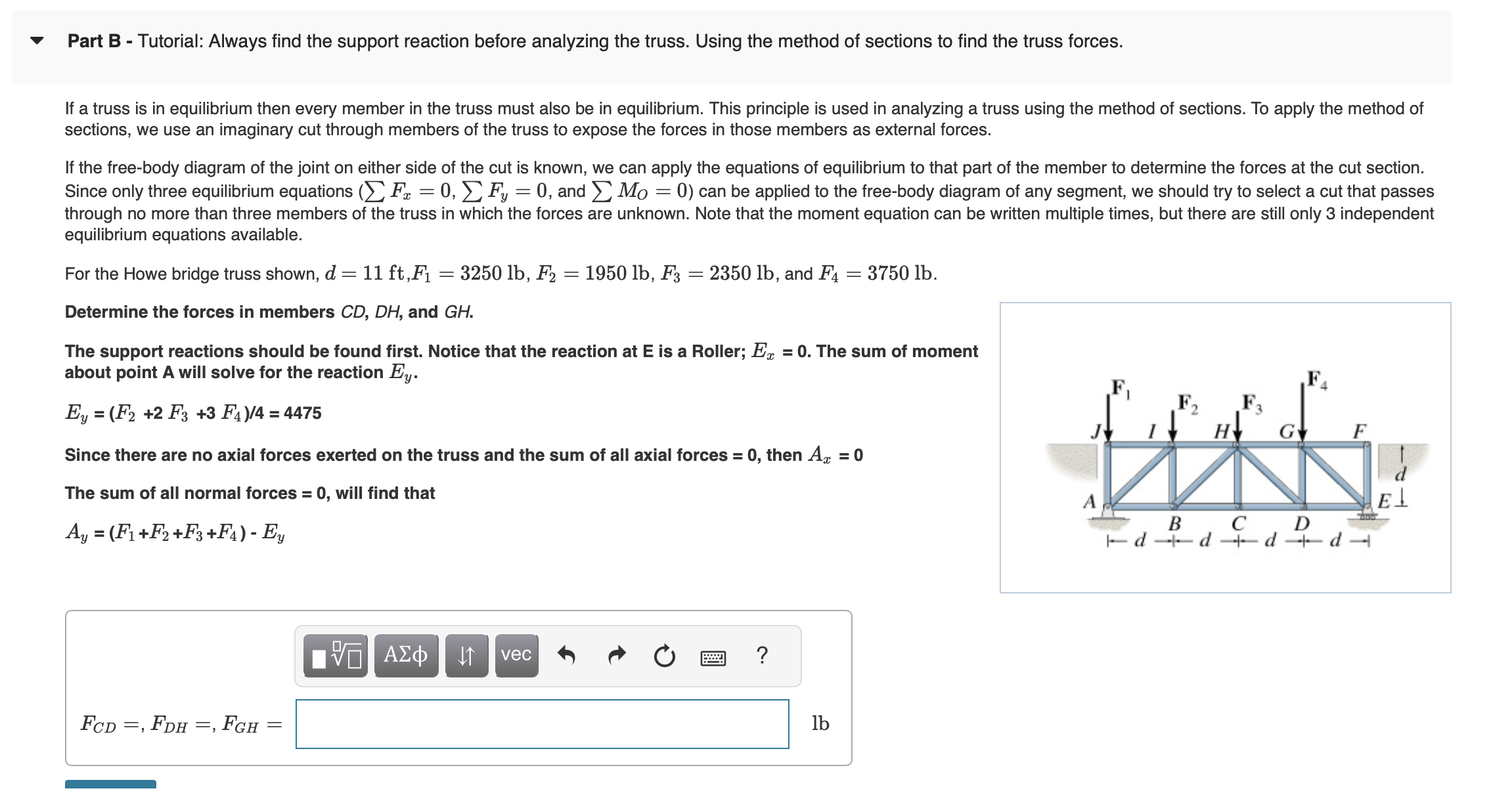
For the Howe bridge truss shown, $d=11ft,F_1=3250lb,F_2=1950lb,F_3=2350lb,$ and $F_4=3750lb.$

Determine the forces in members $CD,DH,$ and $GH.$

The support reactions should be found first. Notice that the reaction at $E$ is a Roller; $E_x=0.$ The sum of moment

about point A will solve for the reaction $E_y.$

$E_y=\frac{F_2+2F_3+3F_4}{4}=4475$

Since there are no axial forces exerted on the truss and the sum of all axial forces $=0,$ then $A_x=0$

The sum of all normal forces $=0,$ will find that

$A_y=(F_1+F_2+F_3+F_4)-E_y$

$F_{CD}=,F_{DH}=,F_{GH}=$