Perform complexity analysis for the algorithm by

(1) find the recurrence equation;

(2) solve the recurrent equation and

(3) conclude on the complexity class for the algorithm by a proof.

Show how the recurrence equation is derived, how it is solved and prove the asymtotic complexity.

Analyze the number of comparisons between array elements

(between min1 and min2 throughout the recursive calls) in terms of n,

the size of the array A. Assume that n = 2^k

int minimum(A[l..r]) {// compute the minimum value in the array A starting from position l till position r // n = r-l+1 and l

if (l == r) return A[ l ]

else {

min1 = minimum(A[ l.. ]);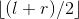

min2 = minimum(A[ (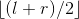+1..r ]);

if (min1

else return min2;

}

}

|(1+r)/2 |(1+r)/2