Perform complexity analysis for the algorithm by

(1) find the recurrence equation;

(2) solve the recurrent equation and

(3) conclude on the complexity class for the algorithm by a proof.

Show how the recurrence equation is derived, how it is solved and prove the asymtotic complexity.

Analyze the number of divisions in terms of n. Assume that n = 2^k

int minimum(A[l..r]) {// compute the minimum value in the array A starting from position l till position r // n = r-l+1 and l

if (l == r) return A[ l ]

else {

min1 = minimum(A[ l.. ]);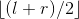

min2 = minimum(A[ (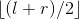+1..r ]);

if (min1 |(1+r)/2 |(1+r)/2 |(1+r)/2 |(1+r)/2