please # 25, 27, 31, 35, 45

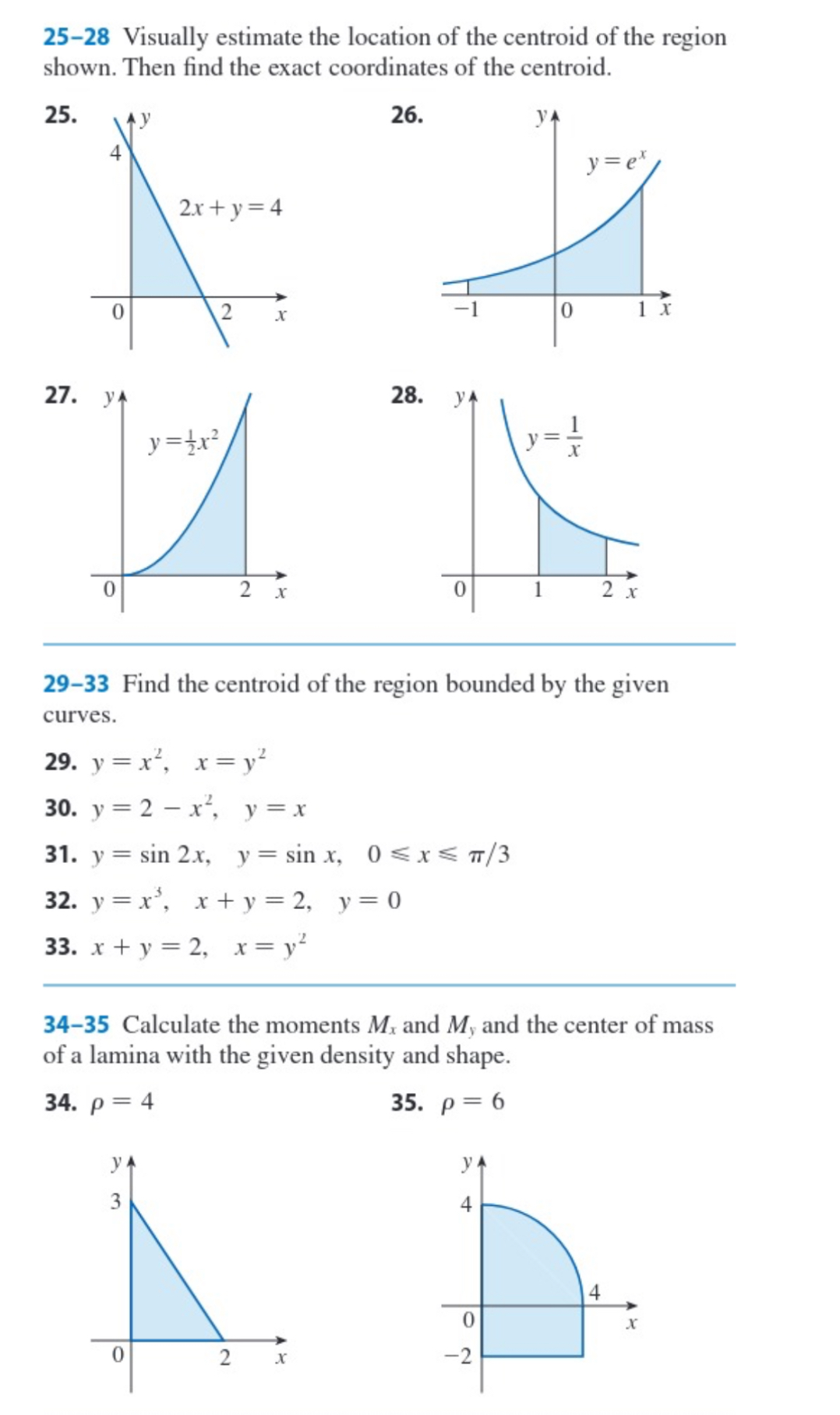
25-28 Visually estimate the location of the centroid of the region shown. Then find the exact coordinates of the centroid. 25. 26. YA 4 y = e 2x+ y =4 0 2 x 10 1 x 27. YA 28. VA y=zx2 y = x x x 29-33 Find the centroid of the region bounded by the given curves. 29. y = x , x=y' 30. y = 2 - x, y =x 31. y = sin 2x, y = sin x, 0 x 7/3 32. y= x', xty =2, y=0 33. x+ y = 2, x=y' 34-35 Calculate the moments Mr and My and the center of mass of a lamina with the given density and shape. 34. p = 4 35. p = 6 YA 3 4 A 0 Y 0 2 x -244-46 Use the Theorem of Pappus to find the volume of the given solid. 44. A sphere of radius r (Use Example 4.) 45. A cone with height h and base radius rEXAMPLE 4 Find the center of mass of a semicircular plate of radius r with uniform density. SOLUTION In order to use (8) we place the semicircle as in Figure 11 so that y= Vr2-x2 f(x) = vr2 - x2 and a = -r, b = r. Here there is no need to use the formula to 4r calculate x because, by the symmetry principle, the center of mass must lie on the 317 y-axis, so x = 0. The area of the semicircle is A = 3 Tr2, so -r 0 X FIGURE 11 = . 1 1, ( voz - xz ) dx 2 = ['(2 - x3 ) dx (since the integrand is even) x' = 3 2 273 4r = 3 3 TT The center of mass is located at the point (0, 4r/(3TT))