Please adapt the given MATLAB script to solve the problem

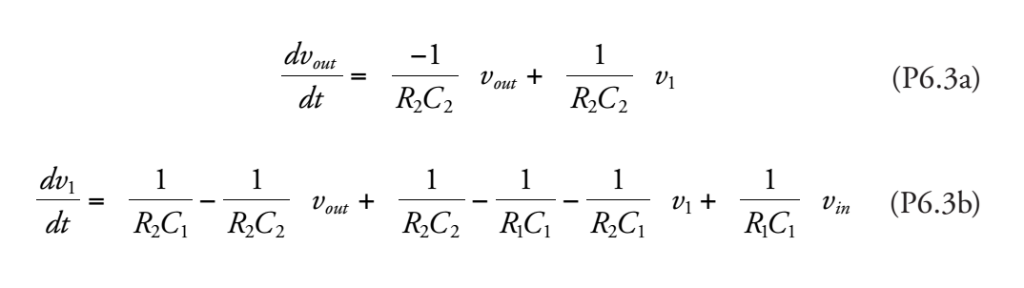
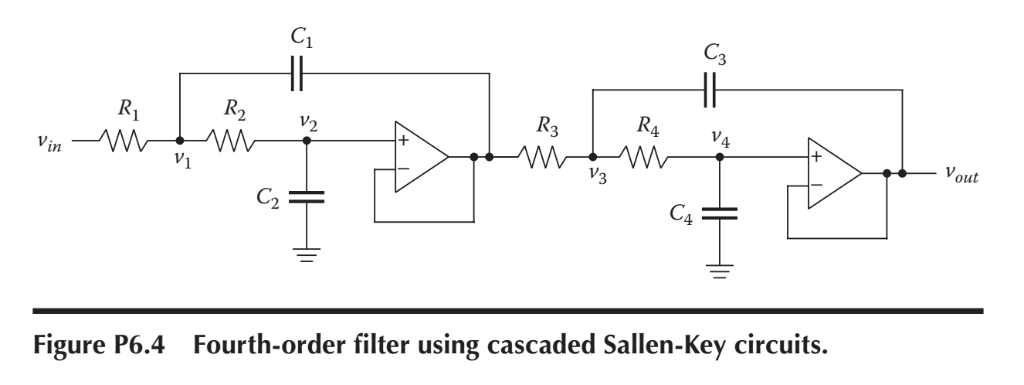
Problem 6.4 By cascading the Sallen-Key circuit, we can create higher-order filters. Figure P6.4 shows an example of a fourth-order filter. Using Equations (P6.3a) and (P6.3b), write a system of four first-order differ- ential equations to describe the fourth-order Sallen-Key circuit. Remember that Vout of the first stage will be equal to Vin of the second stage. Solve for out, using MATLAB's ode45 function. Assume that the input to the circuit vn is a step voltage that changes from 0 V to 1 Vat time t 0.Assume the following values for the circuit elements: R-R2 R R4 G-18000 pF, C2-15000 pF, G-4.7 F, and C4-10 pF. Use a time interval oft= [0, 0.005] o (O) = ui (0)-U2(0)-y(0) = 0 Plot vo, and vn with respect to ton the same set of axes. Sec and assume z duout-1 dv, RC (P6.3a) otut 7 di dtRC RC Vout + v1 + RC (P6.3b) 12 C1 V2 4 out 4 Figure P6.4 Fourth-order filter using cascaded Sallen-Key circuits. %Example 6 4.m % This program solves a single second order ordinary % differential equation by the Runge-Kutta Method. The % differential equation describes the capacitor voltage % in a series RLC circuit clear; clc; % Component values: R-10 L-1.0e-3 C-2.0e-6 % initial conditions: vc (1) 0 v2 (1)-6sqrt (1/ (L c)) % Define time interval and step size. Since the natural % frequency sart(1/LC) is 3559 Hz, choose a time interval % to capture several oscillations. 3559 Hz has period of % 281 usec, so choose 1000 usec for interval. tmax-1000e-6; steps-100; h-tmax/steps ; % Define V2' = f(t,x,y): v2_prime (t, x, y) -(1/(L*C))*x - (R/L)*Y % Do Runge-Kutta algorithm : for i-1:steps K1-v2_prime (t(i), vc(i), v2(i)) L1aV2 (i) ; K2-v2_prime (t (i), vc(i) +h/2*Ll, v2 (i) +h/2*K1) 2-V2 (1) +h/2 *K1 ; K3-v2_prime (t (i), vc(i) +h/2 L2, v2 (i) +h/2*K2) L3sv2 ( i ) +h/2-K2 ; K4-12-prime (t(i), veli) +h*L3, v2 (i) +h*K3 ); L4-12 (i) +htK3 ; vc (1+1)-vc (11+h/6* (L1 +2 *L2 +2 *L3+L4 ) ; V2 (1+1)-V2 (i) +h/6*(K1+2tK2 +2 * K3 + K4 ) ; end % Calculate exact solution beta-v2 (1) / sqrt(1/ (L*C) (R/ (2*L)) 2) vc-exact exp (-R/ (2*L) * t) * beta * sin (sqrt( 1/ (L*c) - (R/ (2*L)) 2)*t % Print results to screen. fprintf 'Runge-Kutta solution for a single' fprintf ('second order ODE: '); fprintf (' R-K Sol''n Exact Sol' 'n ' for 1-1: 10: steps +1 % just print every tenth step fprint f ( ' %10.3e %8.4f %8.4f ' , t (i) vc(i), vc exact (i)) end % Plot results: plot (t, vc exact,t,vc, 'x') xlabel ('t (seconds)', ylabel ('volts') title('Capacitor voltage of series RLC circuit') legend (Exact', 'Runge-Kutta') Problem 6.4 By cascading the Sallen-Key circuit, we can create higher-order filters. Figure P6.4 shows an example of a fourth-order filter. Using Equations (P6.3a) and (P6.3b), write a system of four first-order differ- ential equations to describe the fourth-order Sallen-Key circuit. Remember that Vout of the first stage will be equal to Vin of the second stage. Solve for out, using MATLAB's ode45 function. Assume that the input to the circuit vn is a step voltage that changes from 0 V to 1 Vat time t 0.Assume the following values for the circuit elements: R-R2 R R4 G-18000 pF, C2-15000 pF, G-4.7 F, and C4-10 pF. Use a time interval oft= [0, 0.005] o (O) = ui (0)-U2(0)-y(0) = 0 Plot vo, and vn with respect to ton the same set of axes. Sec and assume z duout-1 dv, RC (P6.3a) otut 7 di dtRC RC Vout + v1 + RC (P6.3b) 12 C1 V2 4 out 4 Figure P6.4 Fourth-order filter using cascaded Sallen-Key circuits. %Example 6 4.m % This program solves a single second order ordinary % differential equation by the Runge-Kutta Method. The % differential equation describes the capacitor voltage % in a series RLC circuit clear; clc; % Component values: R-10 L-1.0e-3 C-2.0e-6 % initial conditions: vc (1) 0 v2 (1)-6sqrt (1/ (L c)) % Define time interval and step size. Since the natural % frequency sart(1/LC) is 3559 Hz, choose a time interval % to capture several oscillations. 3559 Hz has period of % 281 usec, so choose 1000 usec for interval. tmax-1000e-6; steps-100; h-tmax/steps ; % Define V2' = f(t,x,y): v2_prime (t, x, y) -(1/(L*C))*x - (R/L)*Y % Do Runge-Kutta algorithm : for i-1:steps K1-v2_prime (t(i), vc(i), v2(i)) L1aV2 (i) ; K2-v2_prime (t (i), vc(i) +h/2*Ll, v2 (i) +h/2*K1) 2-V2 (1) +h/2 *K1 ; K3-v2_prime (t (i), vc(i) +h/2 L2, v2 (i) +h/2*K2) L3sv2 ( i ) +h/2-K2 ; K4-12-prime (t(i), veli) +h*L3, v2 (i) +h*K3 ); L4-12 (i) +htK3 ; vc (1+1)-vc (11+h/6* (L1 +2 *L2 +2 *L3+L4 ) ; V2 (1+1)-V2 (i) +h/6*(K1+2tK2 +2 * K3 + K4 ) ; end % Calculate exact solution beta-v2 (1) / sqrt(1/ (L*C) (R/ (2*L)) 2) vc-exact exp (-R/ (2*L) * t) * beta * sin (sqrt( 1/ (L*c) - (R/ (2*L)) 2)*t % Print results to screen. fprintf 'Runge-Kutta solution for a single' fprintf ('second order ODE: '); fprintf (' R-K Sol''n Exact Sol' 'n ' for 1-1: 10: steps +1 % just print every tenth step fprint f ( ' %10.3e %8.4f %8.4f ' , t (i) vc(i), vc exact (i)) end % Plot results: plot (t, vc exact,t,vc, 'x') xlabel ('t (seconds)', ylabel ('volts') title('Capacitor voltage of series RLC circuit') legend (Exact', 'Runge-Kutta')