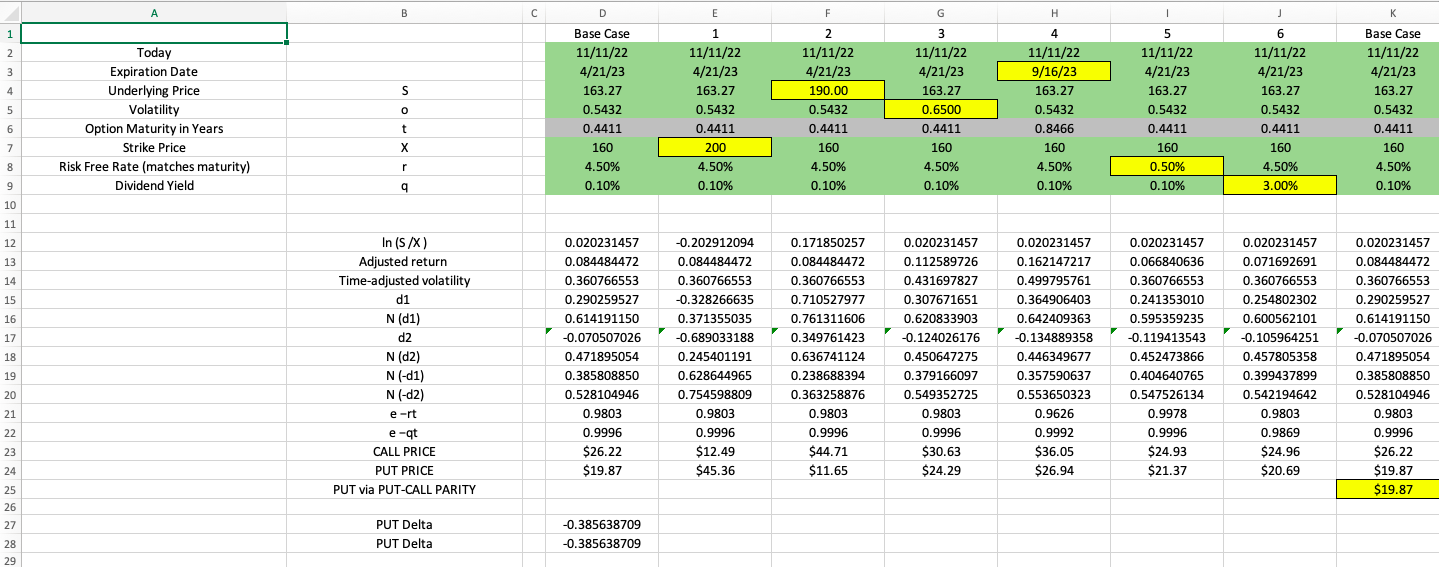
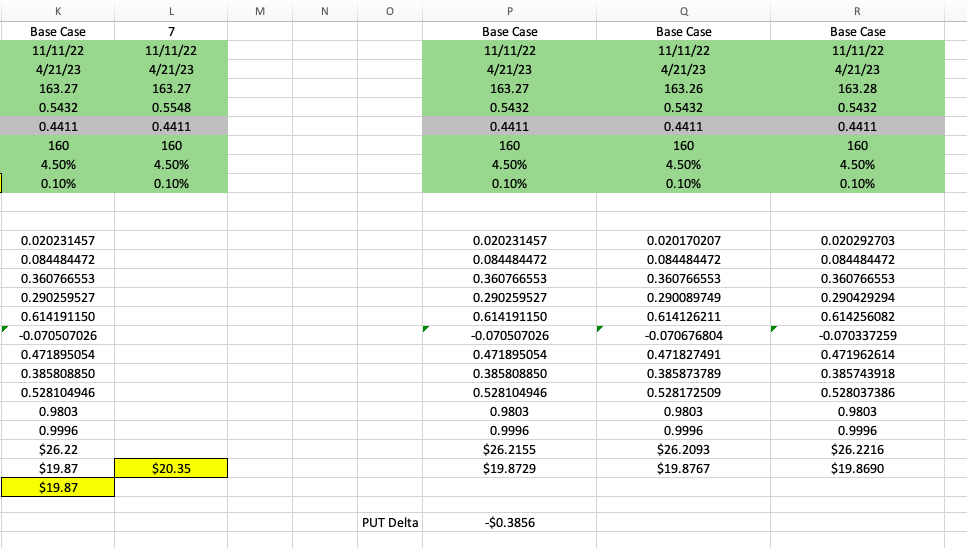
Question: please answer all the empty green cells begin{tabular}{|c|c|} hlineK & L hline Base Case & 7 hline 11/11/22 & 11/11/22 hline 4/21/23
 please answer all the empty green cells
please answer all the empty green cells
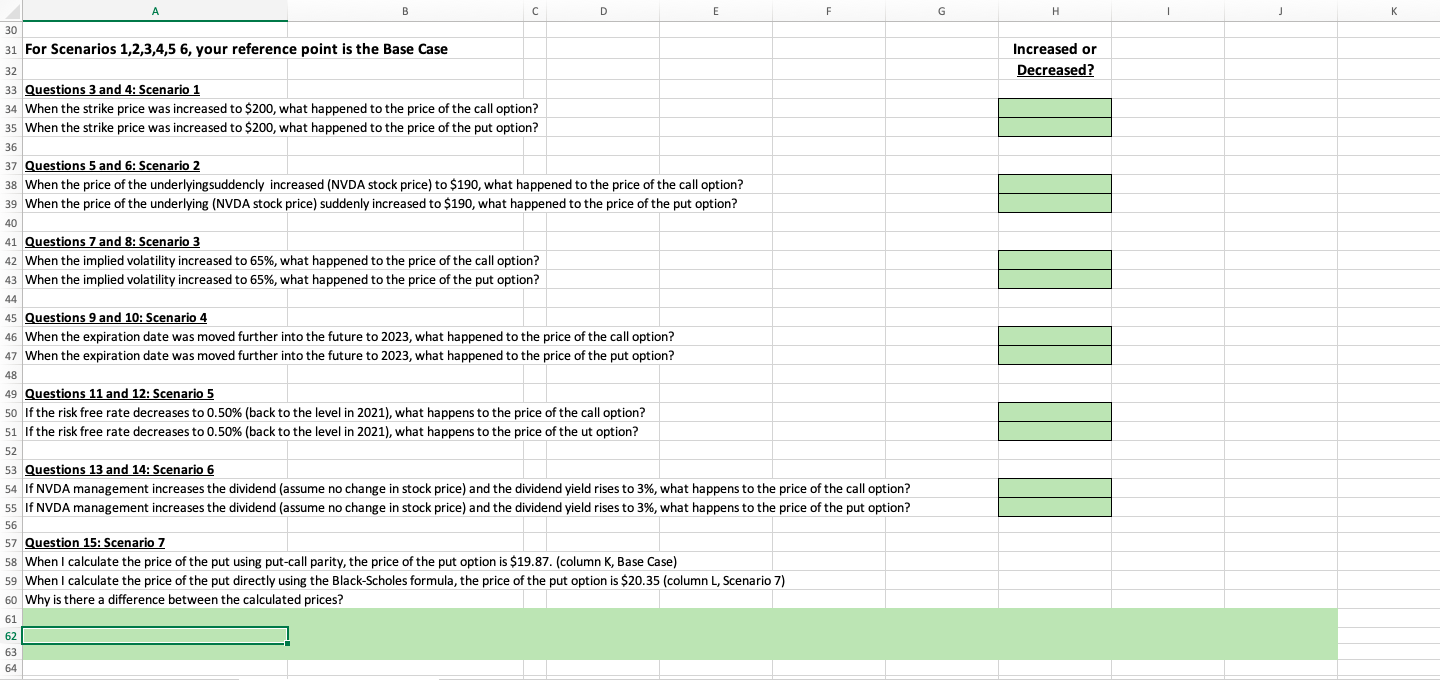
\begin{tabular}{|c|c|} \hlineK & L \\ \hline Base Case & 7 \\ \hline 11/11/22 & 11/11/22 \\ \hline 4/21/23 & 4/21/23 \\ \hline 163.27 & 163.27 \\ \hline 0.5432 & 0.5548 \\ 0.4411 & 0.4411 \\ 160 & 160 \\ \hline 4.50% & 4.50% \\ \hline 0.10% & 0.10% \\ \hline & \\ \hline 0.020231457 & \\ \hline 0.084484472 & \\ \hline 0.360766553 & \\ \hline 0.290259527 & \\ \hline 0.614191150 & \\ \hline0.070507026 & \\ \hline 0.471895054 & \\ \hline 0.385808850 & \\ \hline 0.528104946 & \\ \hline 0.9803 & \\ \hline 0.9996 & \\ \hline$26.22 & \\ \hline$19.87 & \\ \hline$19.87 & \\ \hline \end{tabular} M N R \begin{tabular}{c|c|c} \hline Base Case & Base Case & Base Case \\ 11/11/22 & 11/11/22 & 11/11/22 \\ 4/21/23 & 4/21/23 & 4/21/23 \\ 163.27 & 163.26 & 163.28 \\ 0.5432 & 0.5432 & 0.5432 \\ 0.4411 & 0.4411 & 0.4411 \\ 160 & 160 & 160 \\ 4.50% & 4.50% & 4.50% \\ 0.10% & 0.10% & 0.10% \end{tabular} For Scenarios 1,2,3,4,5 6, your reference point is the Base Case Questions 3 and 4: Scenario 1 When the strike price was increased to $200, what happened to the price of the call option? When the strike price was increased to $200, what happened to the price of the put option? Questions 5 and 6: Scenario 2 When the price of the underlyingsuddencly increased (NVDA stock price) to $190, what happened to the price of the call option? When the price of the underlying (NVDA stock price) suddenly increased to $190, what happened to the price of the put option? Questions 7 and 8: Scenario 3 When the implied volatility increased to 65%, what happened to the price of the call option? When the implied volatility increased to 65%, what happened to the price of the put option? Questions 9 and 10: Scenario 4 When the expiration date was moved further into the future to 2023 , what happened to the price of the call option? When the expiration date was moved further into the future to 2023 , what happened to the price of the put option? Questions 11 and 12: Scenario 5 If the risk free rate decreases to 0.50% (back to the level in 2021), what happens to the price of the call option? If the risk free rate decreases to 0.50% (back to the level in 2021), what happens to the price of the ut option? Questions 13 and 14: Scenario 6 If NVDA management increases the dividend (assume no change in stock price) and the dividend yield rises to 3%, what happens to the price of the call option? If NVDA management increases the dividend (assume no change in stock price) and the dividend yield rises to 3%, what happens to the price of the put option? Question 15: Scenario 7 When I calculate the price of the put using put-call parity, the price of the put option is $19.87. (column K, Base Case) When I calculate the price of the put directly using the Black-Scholes formula, the price of the put option is $20.35 (column L, Scenario 7) Why is there a difference between the calculated prices
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


