please answer asap thank you

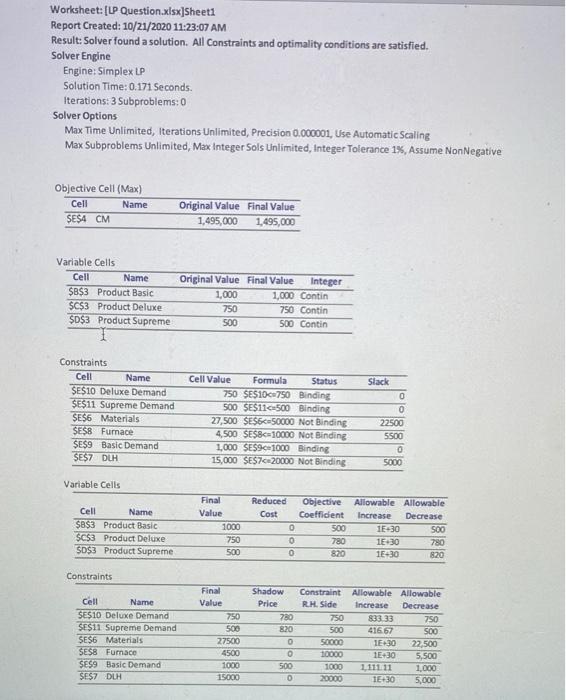
Click to open a Linear Programming report and answer the following questions about it. In your answer, create a bullet point list, in the same order. No need to repeat the question. 1) Describe what the program is trying to accomplish. 2) How many products are under consideration and what are their names? 3) How many constraints are there? 4) How many constraints are impacting the final solution and which ones are they? 5) If we follow the recommendation of the report, how much of the solutions purpose will be generated? 6) What is the shadow price for direct labour hours (DLH)? 7) If we could get another 1,000 direct labour hours, how much would we benefit? 8) If we could find a way to sell an additional 10 Basic units, how much would we benefit? 9) Its recommended that we make 500 Supreme units. Being specific, why is that number being recommended 10) Do you think Linear Programming could be useful to you in the future? Worksheet: [LP Question.xlsx]Sheet1 Report Created: 10/21/2020 11:23:07 AM Result: Solver found a solution. All Constraints and optimality conditions are satisfied, Solver Engine Engine: Simplex LP Solution Time: 0.171 Seconds. Iterations: 3 Subproblems:0 Solver Options Max Time Unlimited, Iterations Unlimited, Precision 0.000001, Use Automatic Scaling Max Subproblems Unlimited, Max Integer Sols Unlimited, Integer Tolerance 1%, Assume NonNegative Objective Cell (Max) Cell Name SE$4 CM Original Value Final Value 1,495,000 1,495,000 Variable Cells Cell Name $B$3 Product Basic $C$3 Product Deluxe $D$3 Product Supreme Original Value Final Value Integer 1,000 1,000 Contin 750 750 Contin 500 500 Contin Name Constraints Cell SE$10 Deluxe Demand $E$11 Supreme Demand SE56 Materials SE$8 Fumace $E$9 Basic Demand SE$7 DUH Cell Value Formula Status 750 SE$10.750 Binding 500 SE$11-500 Binding 27,500 SE$6c-50000 Not Binding 4.500 SE$8c=10000 Not Binding 1,000 SE$9c-1000 Binding 15,000 SES7-20000 Not Binding Slack 0 0 22500 5500 0 5000 Variable Cells Cell Name $8$3 Product Basic $C$3 Product Deluxe SD$3 Product Supreme Final Value 1000 750 500 Reduced Objective Allowable Allowable Cost Coefficient Increase Decrease 0 500 1E+30 500 0 780 15:30 780 0 620 1E430 820 Constraints Cell Name SE$10 Deluxe Demand SE$11 Supreme Demand SE$6 Materials SE$8 Furnace SES9 Basic Demand SES7 DUH Final Value 750 500 27500 4500 1000 15000 Shadow Price 780 820 0 O 500 0 Constraint Allowable Allowable R.H. Side Increase Decrease 750 83333 750 500 41667 SOO 50000 1E30 22,500 10000 1E30 5,500 1000 111111 1.000 20000 1E30 5,000 Click to open a Linear Programming report and answer the following questions about it. In your answer, create a bullet point list, in the same order. No need to repeat the question. 1) Describe what the program is trying to accomplish. 2) How many products are under consideration and what are their names? 3) How many constraints are there? 4) How many constraints are impacting the final solution and which ones are they? 5) If we follow the recommendation of the report, how much of the solutions purpose will be generated? 6) What is the shadow price for direct labour hours (DLH)? 7) If we could get another 1,000 direct labour hours, how much would we benefit? 8) If we could find a way to sell an additional 10 Basic units, how much would we benefit? 9) Its recommended that we make 500 Supreme units. Being specific, why is that number being recommended 10) Do you think Linear Programming could be useful to you in the future? Worksheet: [LP Question.xlsx]Sheet1 Report Created: 10/21/2020 11:23:07 AM Result: Solver found a solution. All Constraints and optimality conditions are satisfied, Solver Engine Engine: Simplex LP Solution Time: 0.171 Seconds. Iterations: 3 Subproblems:0 Solver Options Max Time Unlimited, Iterations Unlimited, Precision 0.000001, Use Automatic Scaling Max Subproblems Unlimited, Max Integer Sols Unlimited, Integer Tolerance 1%, Assume NonNegative Objective Cell (Max) Cell Name SE$4 CM Original Value Final Value 1,495,000 1,495,000 Variable Cells Cell Name $B$3 Product Basic $C$3 Product Deluxe $D$3 Product Supreme Original Value Final Value Integer 1,000 1,000 Contin 750 750 Contin 500 500 Contin Name Constraints Cell SE$10 Deluxe Demand $E$11 Supreme Demand SE56 Materials SE$8 Fumace $E$9 Basic Demand SE$7 DUH Cell Value Formula Status 750 SE$10.750 Binding 500 SE$11-500 Binding 27,500 SE$6c-50000 Not Binding 4.500 SE$8c=10000 Not Binding 1,000 SE$9c-1000 Binding 15,000 SES7-20000 Not Binding Slack 0 0 22500 5500 0 5000 Variable Cells Cell Name $8$3 Product Basic $C$3 Product Deluxe SD$3 Product Supreme Final Value 1000 750 500 Reduced Objective Allowable Allowable Cost Coefficient Increase Decrease 0 500 1E+30 500 0 780 15:30 780 0 620 1E430 820 Constraints Cell Name SE$10 Deluxe Demand SE$11 Supreme Demand SE$6 Materials SE$8 Furnace SES9 Basic Demand SES7 DUH Final Value 750 500 27500 4500 1000 15000 Shadow Price 780 820 0 O 500 0 Constraint Allowable Allowable R.H. Side Increase Decrease 750 83333 750 500 41667 SOO 50000 1E30 22,500 10000 1E30 5,500 1000 111111 1.000 20000 1E30 5,000