please answer q1 and q2

need to calculation process

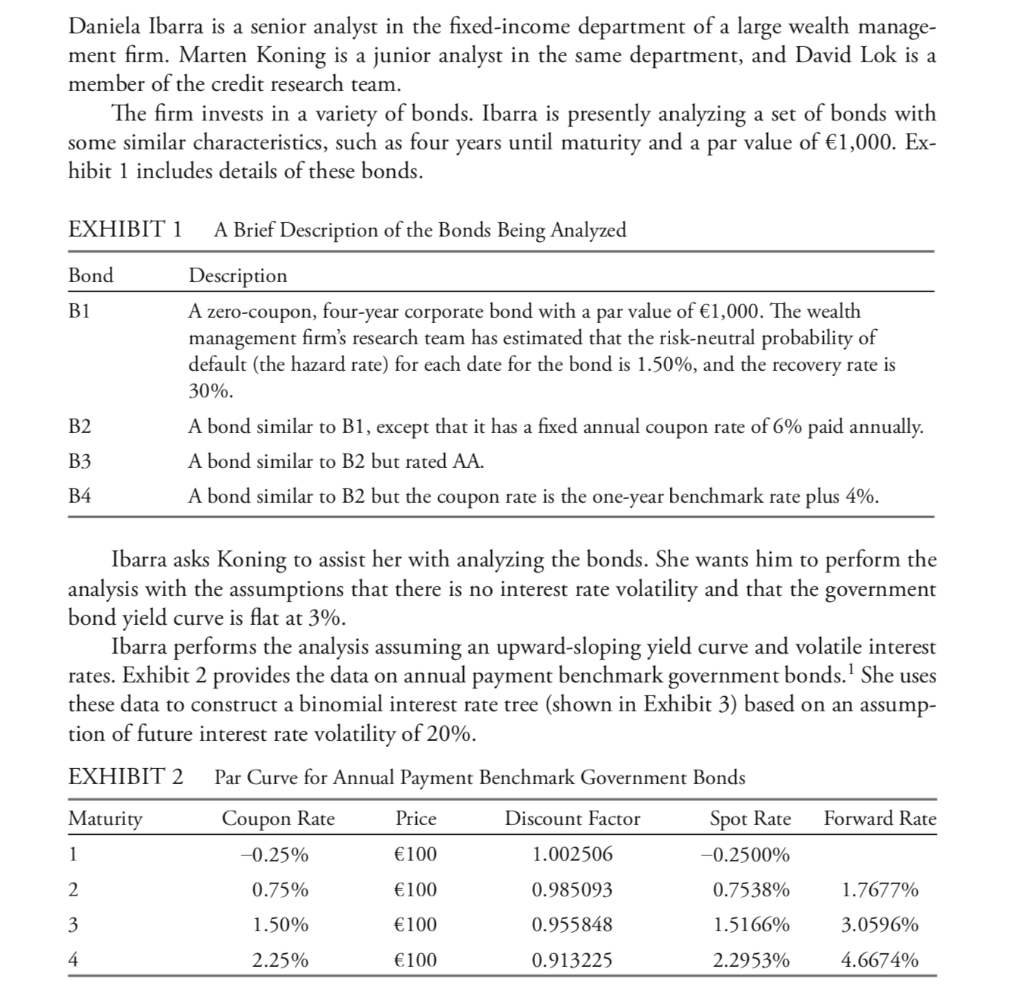
Daniela Ibarra is a senior analyst in the fixed-income department of a large wealth manage- ment firm. Marten Koning is a junior analyst in the same department, and David Lok is a member of the credit research team. The firm invests in a variety of bonds. Ibarra is presently analyzing a set of bonds with some similar characteristics, such as four years until maturity and a par value of 1,000. Ex- hibit 1 includes details of these bonds. EXHIBIT 1 A Brief Description of the Bonds Being Analyzed Bond B1 Description A zero-coupon, four-year corporate bond with a par value of 1,000. The wealth management firm's research team has estimated that the risk-neutral probability of default (the hazard rate) for each date for the bond is 1.50%, and the recovery rate is 30%. A bond similar to B1, except that it has a fixed annual coupon rate of 6% paid annually. A bond similar to B2 but rated AA. A bond similar to B2 but the coupon rate is the one-year benchmark rate plus 4%. B2 B3 B4 Ibarra asks Koning to assist her with analyzing the bonds. She wants him to perform the analysis with the assumptions that there is no interest rate volatility and that the government bond yield curve is flat at 3%. Ibarra performs the analysis assuming an upward-sloping yield curve and volatile interest rates. Exhibit 2 provides the data on annual payment benchmark government bonds. She uses these data to construct a binomial interest rate tree (shown in Exhibit 3) based on an assump- tion of future interest rate volatility of 20%. EXHIBIT 2 Par Curve for Annual Payment Benchmark Government Bonds Maturity Coupon Rate Discount Factor Forward Rate -0.25% 1.002506 -0.2500% Price Spot Rate 1 100 2 0.75% 100 0.985093 0.7538% 1.7677% 3 1.50% 100 0.955848 1.5166% 3.0596% 4 2.25% 100 0.913225 2.2953% 4.6674% EXHIBIT 3 One-Year Binomial Interest Rate Tree for 20% Volatility Date 0 Date 1 Date 2 Date 3 8.0804% (0.1250) 4.3999% (0.2500) 2.1180% (0.5000) 5.4164% (0.3750) -0.2500% (1.000) 2.9493% (0.5000) 1.4197% (0.5000) 3.6307% (0.3750) 1.9770% (0.2500) 2.4338% (0.1250) Answer the first five questions (1-4) based on the assumptions made by Marten Koning, the junior analyst. Answer questions (812) based on the assumptions made by Daniela Ibarra, the senior analyst. Note: All calculations in this problem set are carried out on spreadsheets to preserve preci- sion. The rounded results are reported in the solutions. 1. The market price of bond B1 is 875. The bond is: A. fairly valued. B. overvalued. C. undervalued. 2. Koning realizes that an increase in the recovery rate would lead to an increase in the bond's fair value, whereas an increase in the probability of default would lead to a decrease in the bond's fair value. He is not sure which effect would be greater, however. So, he increases both the recovery rate and the probability of default by 25% of their existing estimates and recomputes the bond's fair value. The recomputed fair value is closest to: A. 843.14. B. 848.00. C. 855.91