Please answer Q4.

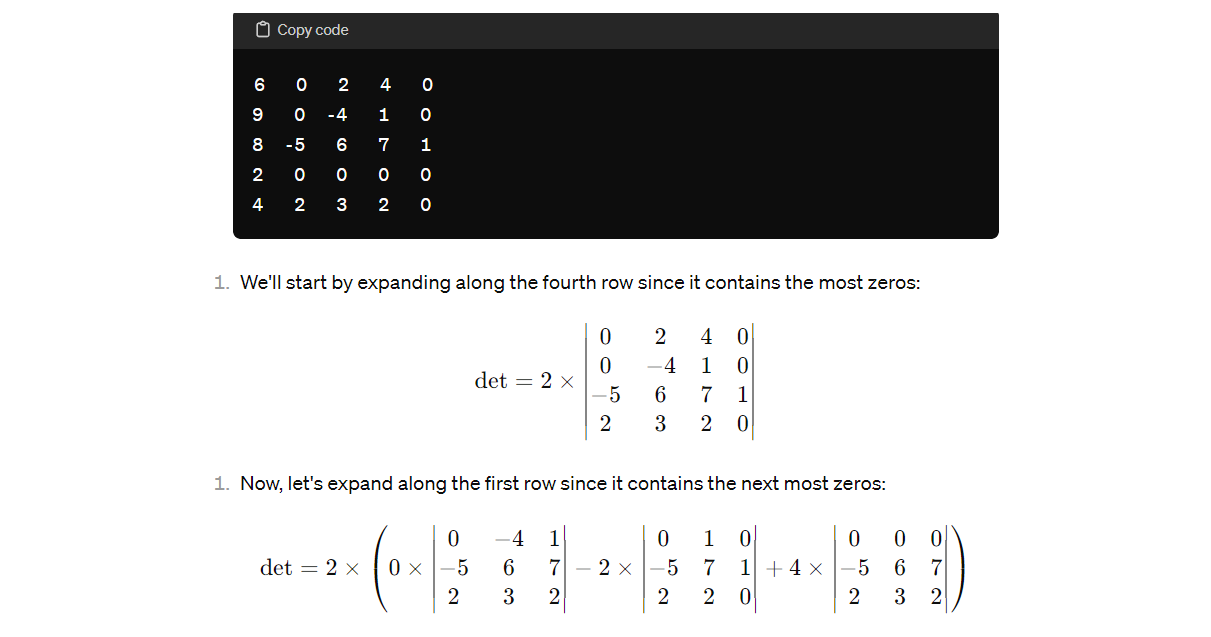
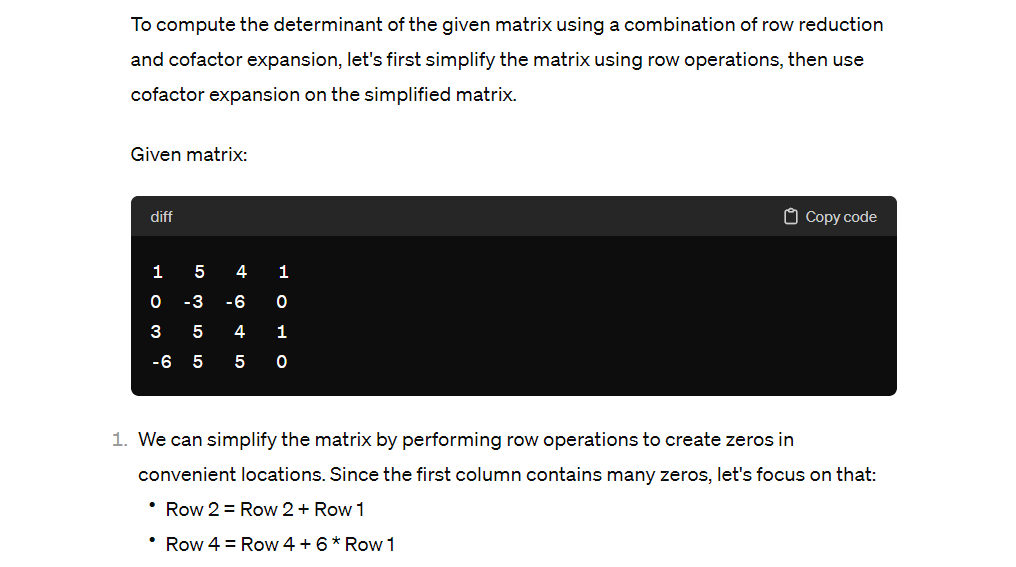
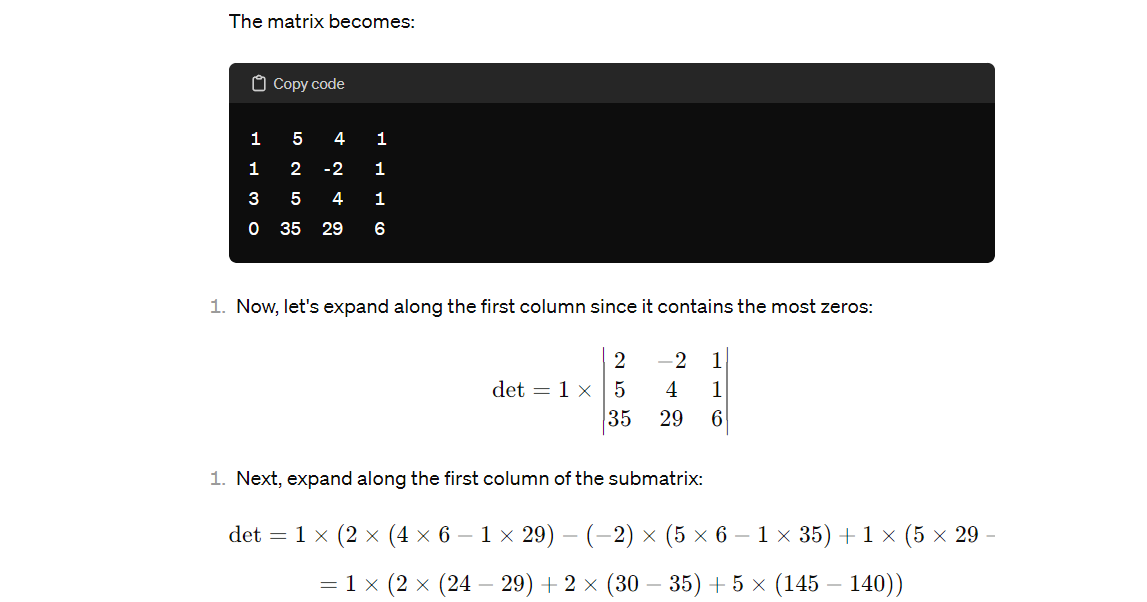
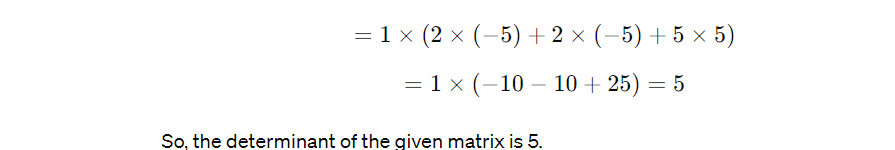
Combine the methods of row reduction and cofactor expansion to compute the determinants in Exercises 11-14. 4 -3 -1 2 1 -3 3 4 11. 12. waoo A a WW 0 0 0+ a a w w -4 3 11 4 -4 4 2 L N 4 WOK -3 OHO - UI AOA OON - 13. 14. 6 -2 -6 6Each equation in Exercises 1-4 illustrates a property of determi nants. State the property. 1. 5 -2 -3 6 O 4 -1 2. N W W = 31 3 WUN win 3. JWN -4 W W N OO A NUR OAN 4. a w W NL NWA WOK14. 13. 11. 9. ANODA OUNOA DOOW Nonoo OOWOO OO NU WONO amount of computation. WOMAN DUANY ONWA HONO NOTHA SNAOW WUWA OOHOO NWOOU 12. 10. Compute the determinants in Exercises 9-14 by cofactor expan- WN YW NNO- sions. At each step, choose a row or column that involves the least CaNO OfON AWOO wwwA WOOD UNION) Copy code 0 2 4 0 0 4 1 0 det =2 x 5 6 7 1 | 2 3 20 Now, let's expand along the first row since it contains the next most zeros: |0 4 1| 01 0 ] det =2 x 1 0 x 5 6 7 2 % 5 7 1| +4 x 5 6 7 2 3 2 2 2 0 2 3 2 0 2 4 0 0 4 1 0 det = 2 x 5 6 7 1 2 3 20 Now, let's expand along the first row since it contains the next most zeros: 0 4 1 0 1 0 0 0 0 det=2x {0x|-5 6 7| 2x|-5 7 1/ +4x|-5 6 7 2 3 2 2 2 0 2 3 2 Now, we expand along the first row of the submatrices: det =2x(0x(-4%x2 1x3) 2x(0x2 1x5)+4x(0x30x =2x(0-2x(-5)+4x0) =2x (10 +0)=20 So, the determinant of the given matrix is 20. To compute the determinant of the given matrix using a combination of row reduction and cofactor expansion, let's first simplify the matrix using row operations, then use cofactor expansion on the simplified matrix. Given matrix: ) Copycode We can simplify the matrix by performing row operations to create zeros in convenient locations. Since the first column contains many zeros, let's focus on that: * Row2=Row 2+ Row 1 * Row4=Row4+6*Row1 The matrix becomes: Copy code 1 5 4 1 1 2 -2 1 3 5 4 1 O 35 29 6 1. Now, let's expand along the first column since it contains the most zeros: 2 -2 det = 1 x 5 4 35 29 6 1. Next, expand along the first column of the submatrix: det = 1 x (2 x (4 x 6 - 1 x 29) - (-2) x (5 x 6 - 1 x 35) + 1 x (5 x 29 =1 x (2 x (24 - 29) + 2 x (30 - 35) + 5 x (145 - 140) )\f