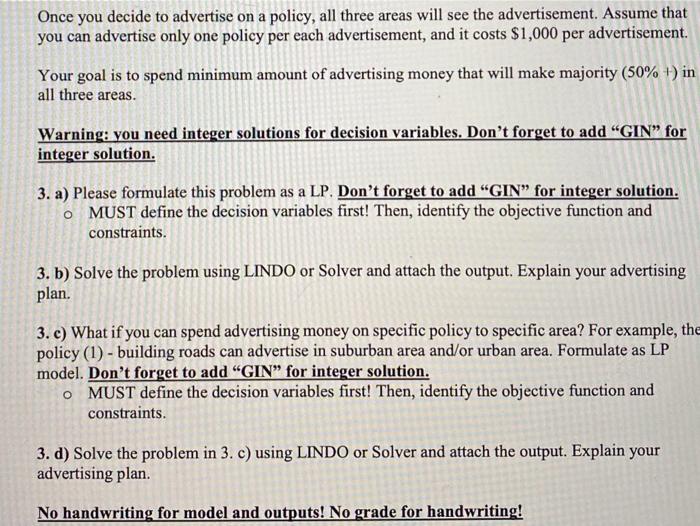
Question: please answer showing all work please answer showing all work 3. LP modeling: Political Campaign Problem: No handwriting for model and outputs! No crade for
please answer showing all work

please answer showing all work
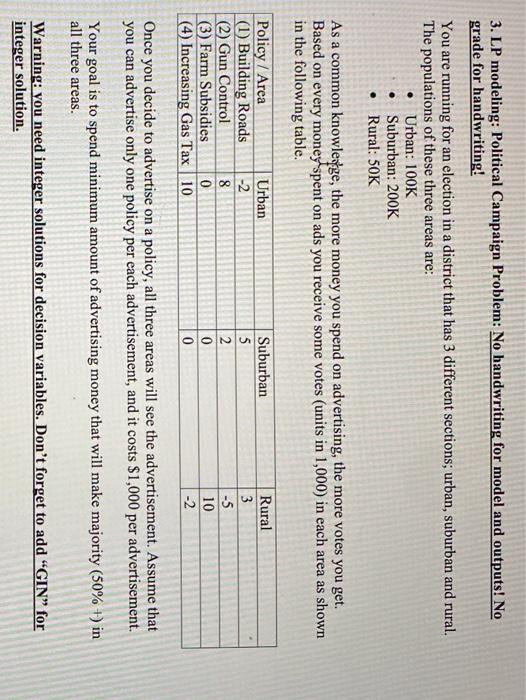
3. LP modeling: Political Campaign Problem: No handwriting for model and outputs! No crade for handwriting! You are running for an election in a district that has 3 different sections, urban, suburban and rural The populations of these three areas are: Urban: 100K Suburban: 200K Rural: SOK As a common knowledge, the more money you spend on advertising, the more votes you get Based on every money spent on ads you receive some votes (units in 1,000) in each area as shown in the following table Policy / Area Urban LU Building Roads (2) Gun Control 8 (3) Farm Subsidies 0 () Increasing Gas Tax 10 Suburban 5 2 Rural 3 5 10 0 Once you decide to advertise on a policy, all three areas will see the advertisement. Assume that you can advertise only one policy per each advertisement, and it costs $1,000 per advertisement Your goal is to spend minimum amount of advertising money that will make majority (50%) in all three areas. Warning you need Integer solutions for decision variables. Don't forget to add "GIN" for integer solution 3. a) Please formulate this problem as a LP Don't forget to add "GIN" for integer solution. MUST define the decision variables first! Then, identify the objective function and constraints 3, b) Solve the problem using LINDO or Solver and attach the output. Explain your advertising plan. 3. c) What if you can spend advertising money on specific policy to specific area? For example, the policy (1) - building roads can advertise in suburban area and/or urban area. Formulate as LP model. Don't forget to add "GIN" for integer solution. MUST define the decision variables first! Then, identify the objective function and constraints. 3. d) Solve the problem in 3. c) using LINDO or Solver and attach the output. Explain your advertising plan No handwriting for model and outputs No grade for handwriting! 3. LP modeling: Political Campaign Problem: No handwriting for model and outputs! No grade for handwriting! You are running for an election in a district that has 3 different sections; urban, suburban and rural. The populations of these three areas are: Urban: 100K Suburban: 200K Rural: 50K As a common knowleyge, the more money you spend on advertising, the more votes you get. Based on every money spent on ads you receive some votes (units in 1,000) in each area as shown in the following table. Policy / Area Urban (1) Building Roads -2 (2) Gun Control 8 (3) Farm Subsidies 0 (4) Increasing Gas Tax 10 Suburban 5 2 0 0 Rural 3 -5 10 -2 Once you decide to advertise on a policy, all three areas will see the advertisement. Assume that you can advertise only one policy per each advertisement, and it costs $1,000 per advertisement Your goal is to spend minimum amount of advertising money that will make majority (50% +) in all three areas. Warning: you need integer solutions for decision variables. Don't forget to add "GIN for integer solution. Once you decide to advertise on a policy, all three areas will see the advertisement. Assume that you can advertise only one policy per each advertisement, and it costs $1,000 per advertisement Your goal is to spend minimum amount of advertising money that will make majority (50% +) in all three areas. Warning: you need integer solutions for decision variables. Don't forget to add GIN for integer solution. 3. a) Please formulate this problem as a LP. Don't forget to add "GIN for integer solution. O MUST define the decision variables first! Then, identify the objective function and constraints. 3. b) Solve the problem using LINDO or Solver and attach the output. Explain your advertising plan. 3. c) What if you can spend advertising money on specific policy to specific area? For example, the policy (1) - building roads can advertise in suburban area and/or urban area. Formulate as LP model. Don't forget to add "GIN for integer solution. O MUST define the decision variables first! Then, identify the objective function and constraints. 3. d) Solve the problem in 3. c) using LINDO or Solver and attach the output. Explain your advertising plan. No handwriting for model and outputs! No grade for handwriting! 3. LP modeling: Political Campaign Problem: No handwriting for model and outputs! No grade for handwriting! You are running for an election in a district that has 3 different sections, urban, suburban and rural. The populations of these three areas are: Urban: 100K Suburban: 200K Rural: 50K As a common knowledge, the more money you spend on advertising, the more votes you get. Based on every money spent on ads you receive some votes (units in 1,000) in each area as shown in the following table. -2 Policy / Area Urban (1) Building Roads (2) Gun Control 8 (3) Farm Subsidies 0 (4) Increasing Gas Tax 10 Suburban 5 2 0 0 Rural 3 -5 10 -2 Once you decide to advertise on a policy, all three areas will see the advertisement. Assume that you can advertise only one policy per each advertisement, and it costs $1,000 per advertisement. Your goal is to spend minimum amount of advertising money that will make majority (50% +) in all three areas. Warning: you need integer solutions for decision variables. Don't forget to add "GIN for integer solution. Once you decide to advertise on a policy, all three areas will see the advertisement. Assume that you can advertise only one policy per each advertisement, and it costs $1,000 per advertisement. Your goal is to spend minimum amount of advertising money that will make majority (50% +) in all three areas. Warning: you need integer solutions for decision variables. Don't forget to add "GIN for integer solution. 3. a) Please formulate this problem as a LP. Don't forget to add "GIN for integer solution. o MUST define the decision variables first! Then, identify the objective function and constraints. 3.b) Solve the problem using LINDO or Solver and attach the output. Explain your advertising plan. 3. e) What if you can spend advertising money on specific policy to specific area? For example, the policy (1) - building roads can advertise in suburban area and/or urban area. Formulate as LP model. Don't forget to add "GIN for integer solution. O MUST define the decision variables first! Then, identify the objective function and constraints. 3. d) Solve the problem in 3. c) using LINDO or Solver and attach the output. Explain your advertising plan. No handwriting for model and outputs! No grade for handwriting! 3. LP modeling: Political Campaign Problem: No handwriting for model and outputs! No crade for handwriting! You are running for an election in a district that has 3 different sections, urban, suburban and rural The populations of these three areas are: Urban: 100K Suburban: 200K Rural: SOK As a common knowledge, the more money you spend on advertising, the more votes you get Based on every money spent on ads you receive some votes (units in 1,000) in each area as shown in the following table Policy / Area Urban LU Building Roads (2) Gun Control 8 (3) Farm Subsidies 0 () Increasing Gas Tax 10 Suburban 5 2 Rural 3 5 10 0 Once you decide to advertise on a policy, all three areas will see the advertisement. Assume that you can advertise only one policy per each advertisement, and it costs $1,000 per advertisement Your goal is to spend minimum amount of advertising money that will make majority (50%) in all three areas. Warning you need Integer solutions for decision variables. Don't forget to add "GIN" for integer solution 3. a) Please formulate this problem as a LP Don't forget to add "GIN" for integer solution. MUST define the decision variables first! Then, identify the objective function and constraints 3, b) Solve the problem using LINDO or Solver and attach the output. Explain your advertising plan. 3. c) What if you can spend advertising money on specific policy to specific area? For example, the policy (1) - building roads can advertise in suburban area and/or urban area. Formulate as LP model. Don't forget to add "GIN" for integer solution. MUST define the decision variables first! Then, identify the objective function and constraints. 3. d) Solve the problem in 3. c) using LINDO or Solver and attach the output. Explain your advertising plan No handwriting for model and outputs No grade for handwriting! 3. LP modeling: Political Campaign Problem: No handwriting for model and outputs! No grade for handwriting! You are running for an election in a district that has 3 different sections; urban, suburban and rural. The populations of these three areas are: Urban: 100K Suburban: 200K Rural: 50K As a common knowleyge, the more money you spend on advertising, the more votes you get. Based on every money spent on ads you receive some votes (units in 1,000) in each area as shown in the following table. Policy / Area Urban (1) Building Roads -2 (2) Gun Control 8 (3) Farm Subsidies 0 (4) Increasing Gas Tax 10 Suburban 5 2 0 0 Rural 3 -5 10 -2 Once you decide to advertise on a policy, all three areas will see the advertisement. Assume that you can advertise only one policy per each advertisement, and it costs $1,000 per advertisement Your goal is to spend minimum amount of advertising money that will make majority (50% +) in all three areas. Warning: you need integer solutions for decision variables. Don't forget to add "GIN for integer solution. Once you decide to advertise on a policy, all three areas will see the advertisement. Assume that you can advertise only one policy per each advertisement, and it costs $1,000 per advertisement Your goal is to spend minimum amount of advertising money that will make majority (50% +) in all three areas. Warning: you need integer solutions for decision variables. Don't forget to add GIN for integer solution. 3. a) Please formulate this problem as a LP. Don't forget to add "GIN for integer solution. O MUST define the decision variables first! Then, identify the objective function and constraints. 3. b) Solve the problem using LINDO or Solver and attach the output. Explain your advertising plan. 3. c) What if you can spend advertising money on specific policy to specific area? For example, the policy (1) - building roads can advertise in suburban area and/or urban area. Formulate as LP model. Don't forget to add "GIN for integer solution. O MUST define the decision variables first! Then, identify the objective function and constraints. 3. d) Solve the problem in 3. c) using LINDO or Solver and attach the output. Explain your advertising plan. No handwriting for model and outputs! No grade for handwriting! 3. LP modeling: Political Campaign Problem: No handwriting for model and outputs! No grade for handwriting! You are running for an election in a district that has 3 different sections, urban, suburban and rural. The populations of these three areas are: Urban: 100K Suburban: 200K Rural: 50K As a common knowledge, the more money you spend on advertising, the more votes you get. Based on every money spent on ads you receive some votes (units in 1,000) in each area as shown in the following table. -2 Policy / Area Urban (1) Building Roads (2) Gun Control 8 (3) Farm Subsidies 0 (4) Increasing Gas Tax 10 Suburban 5 2 0 0 Rural 3 -5 10 -2 Once you decide to advertise on a policy, all three areas will see the advertisement. Assume that you can advertise only one policy per each advertisement, and it costs $1,000 per advertisement. Your goal is to spend minimum amount of advertising money that will make majority (50% +) in all three areas. Warning: you need integer solutions for decision variables. Don't forget to add "GIN for integer solution. Once you decide to advertise on a policy, all three areas will see the advertisement. Assume that you can advertise only one policy per each advertisement, and it costs $1,000 per advertisement. Your goal is to spend minimum amount of advertising money that will make majority (50% +) in all three areas. Warning: you need integer solutions for decision variables. Don't forget to add "GIN for integer solution. 3. a) Please formulate this problem as a LP. Don't forget to add "GIN for integer solution. o MUST define the decision variables first! Then, identify the objective function and constraints. 3.b) Solve the problem using LINDO or Solver and attach the output. Explain your advertising plan. 3. e) What if you can spend advertising money on specific policy to specific area? For example, the policy (1) - building roads can advertise in suburban area and/or urban area. Formulate as LP model. Don't forget to add "GIN for integer solution. O MUST define the decision variables first! Then, identify the objective function and constraints. 3. d) Solve the problem in 3. c) using LINDO or Solver and attach the output. Explain your advertising plan. No handwriting for model and outputs! No grade for handwriting