Please answer the first question according to the answer format of the example question.

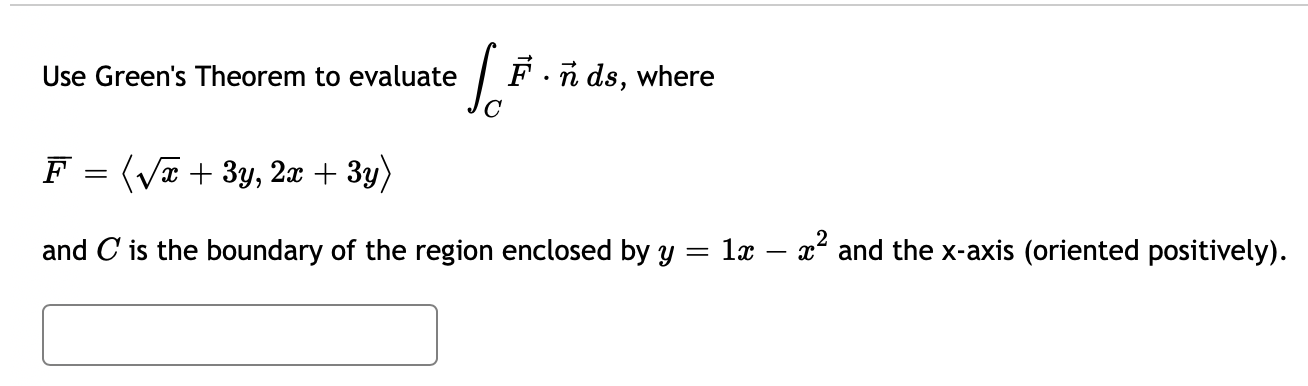
11' Let D be an ellipse rotated counterclockwise by E radians, as pictured below. Before rotation, the horizontal radius was 3 and vertical radius was 4. Convert ff ( 4a: 6y)dA into an integral over a polar integral over a unit circle. (type theta for 9) D Zr 1 f f M 0 0 Use Green's Theorem to evaluate / I?" ~ (1?, where C = and C consists of the arc of the curve 3; = 1:1: 3:2 from (0,0) to (1,0) and the line segment from (1,0) to (0,0). Hint: Check the orientation of the curve before applying the theorem. Use Green's Theorem to evaluate / I; ' ii d3, where C F: and C is the boundary of the region enclosed by y = 1:1: 3:2 l:] and the x-axis (oriented positively). Use Green's Theorem to evaluate: fiat? C where F. = ( + 631,41: + By) and C is the boundary of the region enclosed by y = 3:1: m2 and the 3: -axis (oriented positively). Use Green's Theorem to evaluate: F . n ds C where F = (va + 6y, 4x + 6y) and C is the boundary of the region enclosed by y = 3x - x and the x -axis (oriented positively).11' Let D be an ellipse rotated counterclockwise by E radians, as pictured below. Before rotation, the horizontal radius was 3 and vertical radius was 4. Convert / (_ 83 + 6y)dA into an integral over a polar integral over a unit circle. (type theta for 3) D [27 0\" (3( 4\\/_+3)rcos(9) +4 3\\/_+4)rs1n )()12)r drdB