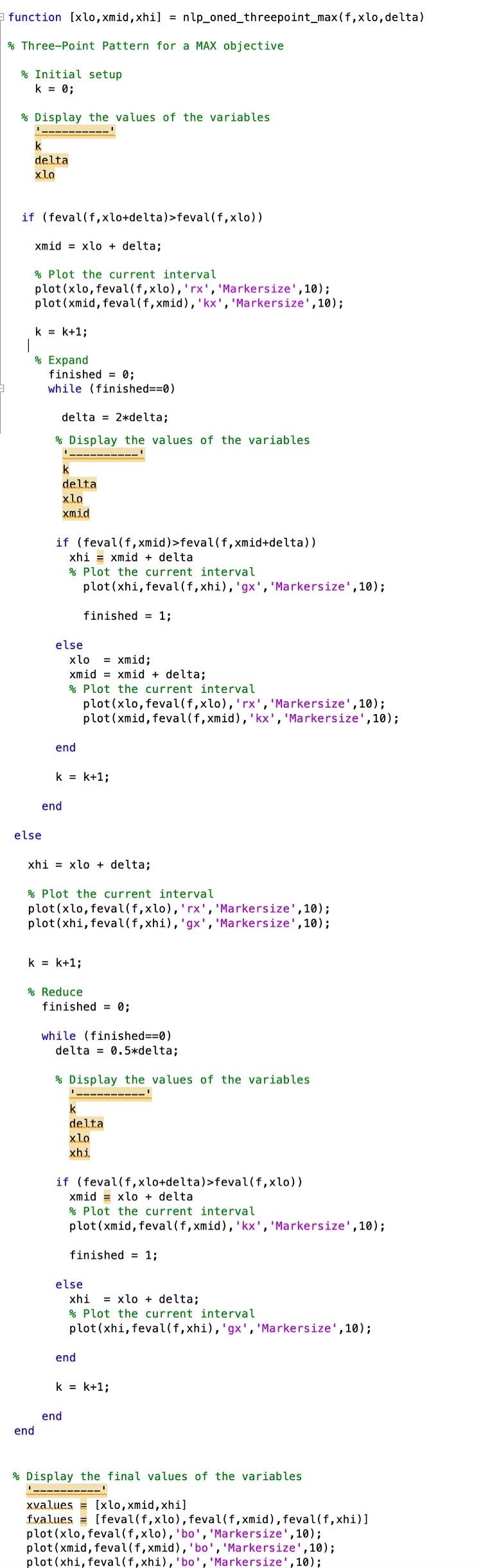
4. Three-Point Patterns Given a lower bound xlo, we are now going to look for a 3-point pattern using the algorithm given in the lectures. Download nlp_oned_threepoint_max.m Download nlp_oned_threepoint_min.m The first line of the function nlp_oned_threepoint_max.mis function [xlo, xmid, xhi] nlp_oned threepoint_max (f, xlo, delta) which outputs the required 3-point pattern. f = @(x) func_oned (x) clf; hold on; [lo, mid, hi] = nlp_oned_threepoint_max (f,0,0.1) Again, the progress of the algorithm is plotted on the graph. The red crosses are the successive values of xlo, the black crosses are the successive values of xmid and the green crosses are the successive values of xhi. Many of the crosses may be drawn in the following iteration, so you are likely to see lots of red crosses or lots of green crosses. The blue circles are the final 3-point pattern. (Keep in mind how the three function-values need to relate to each other in the separate cases of minimize and maximize problems.) Tasks 1. Experiment with different xlo values to initiate the 3-point pattern. What do you observe? (You may need "Ctrl+c" to terminate an infinite loop.) What condition must we put on xlo so that the algorithm can successfully find a 3-point pattern? 2. [30 marks] Experiment with function f =2x10x2 +8 Find a valid 3-point pattern for maximization and a valid 3-point pattern for minimization. (You may need "Ctrl+c" to terminate an infinite loop.) Were you successful with all choices of xlo and delta? Why sometimes it doesn't stop? What xlo and delta combination was the best one in your experiments? What are good choices of xlo and delta in a generic case (with an unknown function)? Why? function [xlo, xmid, xhi] = nlp_oned_threepoint_max (f,xlo, delta) % Three-Point Pattern for a MAX objective % Initial setup k = 0; % Display the values of the variables k delta xlo if (feval(f,xlo+delta)>feval(f,xlo)) xmid xlo + delta;B % Plot the current interval plot (xlo, feval(f,xlo), 'rx', 'Markersize', 10); plot (xmid, feval(f, xmid), 'kx', 'Markersize', 10); k = k+1; % Expand finished = 0; while (finished ==0) delta 2*delta; % Display the values of the variables else k delta xlo xmi.d if (feval(f, xmid)>feval(f, xmid+delta)) xhi xmid + delta % Plot the current interval else plot (xhi, feval(f,xhi), 'gx', 'Markersize', 10); finished = 1; xlo = xmid; xmid xmid + delta;B % Plot the current interval end plot(xlo, feval(f,xlo), 'rx', 'Markersize', 10); plot(xmid, feval(f, xmid), 'kx', 'Markersize', 10); k = k+1; end xhi xlo + delta;B % Plot the current interval plot(xlo, feval(f,xlo), 'rx', 'Markersize',10); plot(xhi, feval(f,xhi), 'gx', 'Markersize', 10); k = k+1; % Reduce finished = 0; while (finished ==0) delta = 0.5*delta; % Display the values of the variables k delta xlo xhi. if (feval(f, xlo+delta)>feval(f,xlo)) xmid xlo + delta % Plot the current interval plot(xmid, feval(f, xmid), 'kx', 'Markersize',10); finished = 1; else xhi xlo + delta;B % Plot the current interval plot(xhi, feval(f,xhi), 'gx', 'Markersize',10); end k = k+1; end end Display the final values of the variables xvalues [xlo, xmid, xhi] fvalues = [feval(f,xlo), feval(f, xmid), feval(f, xhi)] plot (xlo, feval(f,xlo), 'bo', 'Markersize', 10); plot (xmid, feval(f, xmid), 'bo', 'Markersize', 10); plot (xhi, feval(f,xhi), 'bo', 'Markersize',10);