Please answer the question fully

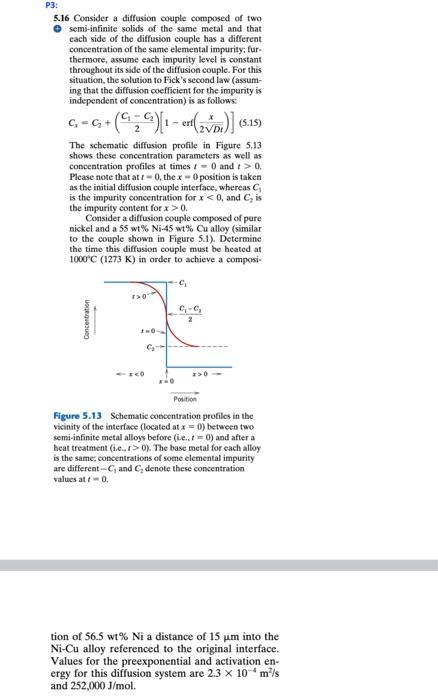
5.16 Consider a diffusion couple composed of two ( semi-infinite solids of the same metal and that each side of the diffusion couple has a different concentration of the same elemental impurity; furthermore, assume each impurity level is constant throughout its side of the diffusion couple. For this situation, the solution to Fick's second law (assuming that the diffusion coefficient for the impurity is independent of concentration) is as follows: Cx=C2+(2C1C2)[1erf(2Dtx)](5.15) The schematic diffusion profile in Figure 5.13 shows these concentration parameters as well as concentration profiles at times t=0 and t>0. Please note that at t=0, the x=0 position is taken as the initial diffusion couple interface, whereas C1 is the impurity concentration for x0. Consider a diffusion couple composed of pare nickel and a 55 wt\% Ni.45 wt\% Cu alloy (similar to the couple shown in Figure 5.1). Determine the time this diffusion couple must be heated at 1000C(1273K) in order to achieve a composi- Figure 5.13 Schematic concentration profiles in the vicinity of the interface (located at x=0 ) between two semi-infinite metal alloys before (i.e. t=0 ) and after a heat treatment (i.e., t>0 ). The base metal for each alloy is the same; concentrations of some elemental impurity are differeat C1 and C2 denote these concentration values at t=0. tion of 56.5wt%Ni a distance of 15m into the NiCu alloy referenced to the original interface. Values for the preexponential and activation energy for this diffusion system are 2.3104m2/s and 252,000J/mol