please answer the questions

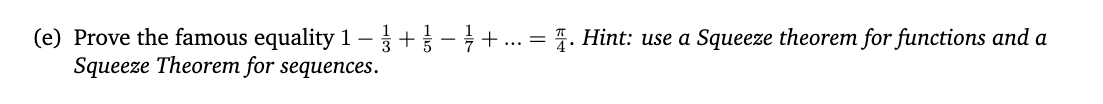
Computing the actual value of a convergent series can be a very complicated problem. The value of some series is so astounding that they have become famous in the history of mathematics, for instance: 00 Euler's 2 3;; = \"g. Here we will prove another following famous equality using power series: n=1 1 1+1 1+ _ 3 5 7 \""4 (a) Compute the power series S (m) of arctan(m). :1 (b) Find the radius of convergence of 8(a) and its interval of convergence. Does the series 3(1) converge? Hint: you may want to use two di'erent tests for convergence of series. (c) Use a theorem to justify that 151%) = %. Does the same theorem allow you to say 8(1) = ? Justify your answer. (d) Let PN(:1:) be the N -th Taylor polynomial of arctan(m). Show that for all N e N and a: 6 (0,1), we have: P4N+3(3?) S motam) S P4N+1(m) (e) Prove the famous equality 1 % + % % + = {a Hint: use a Squeeze theorem for functions and a Squeeze Theorem for sequences