Your help is appreciated, steps are welcome

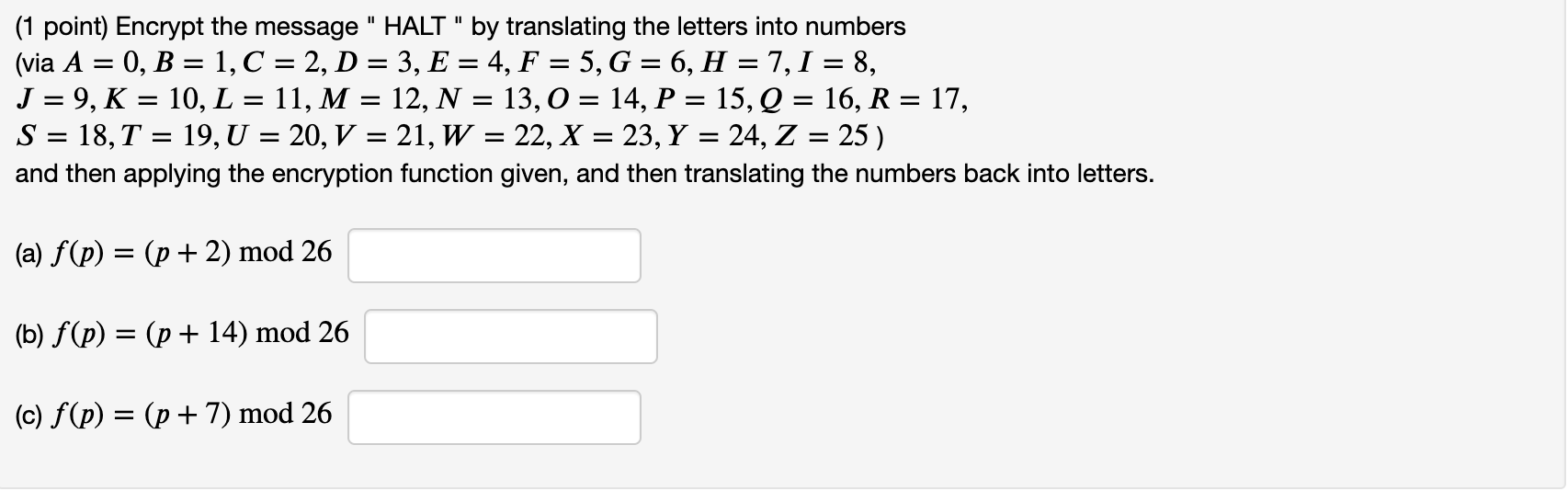
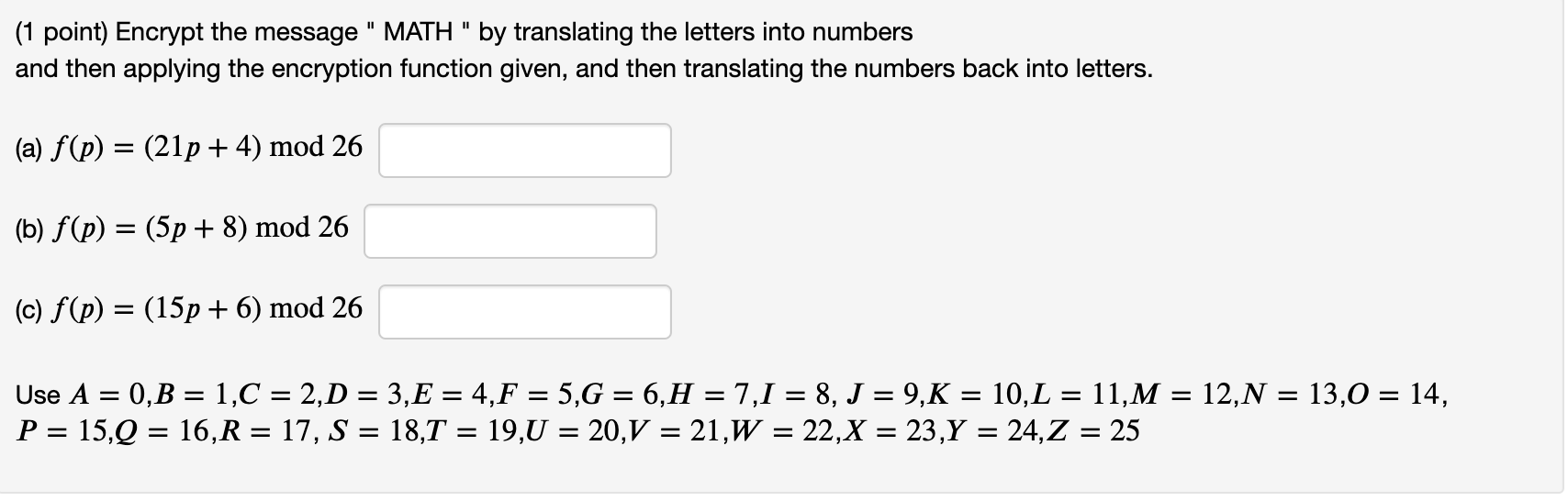
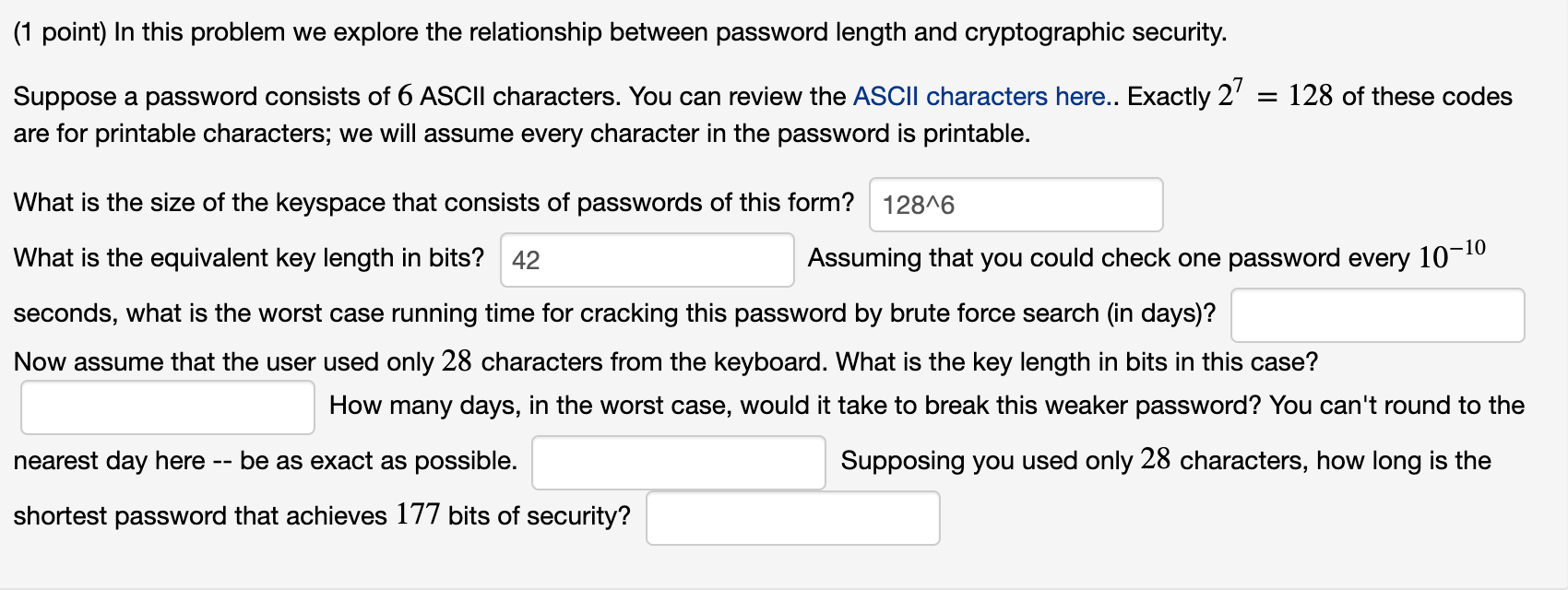
(1 point) Encrypt the message " HALT" by translating the letters into numbers (via A = 0, B = 1, C = 2, D= 3, E = 4, F = 5, G = 6, H = 7,1 = 8, J = 9, K = 10, L = 11, M = 12, N = 13,0 = 14, P = 15, Q = 16, R = 17, S = 18, T = 19, U = 20, V = 21, W = 22, X = 23, Y = 24, Z = 25 ) and then applying the encryption function given, and then translating the numbers back into letters. (a) f(p) = (p + 2) mod 26 (b) f(p) = (p + 14) mod 26 (c) f(p) = (p + 7) mod 26 (1 point) Encrypt the message " MATH " by translating the letters into numbers and then applying the encryption function given, and then translating the numbers back into letters. (a) f(p) = (21p + 4) mod 26 (b) f(p) = (5p + 8) mod 26 (c) f(p) = (15p + 6) mod 26 Use A = 0,B = 1,C = 2,D = 3,E = 4,F = 5,6 = 6,H = 7,1 = 8, J = 9,K = 10,L = 11,M = 12,N = 13,0 = 14, P = 15,Q = 16,R = 17, S = 18,7 = 19,0 = 20,V = 21,W = 22,X = 23,Y = 24, Z = 25 (1 point) Decrypt the message RJAPHWJTO which was encrypted using the affine cipher: f(p) = (11p +9) mod 26 Alphabet: A = 0, B = 1, ... , Z = 25 Message: (1 point) In this problem we explore the relationship between password length and cryptographic security. Suppose a password consists of 6 ASCII characters. You can review the ASCII characters here.. Exactly 27 = 128 of these codes are for printable characters; we will assume every character in the password is printable. What is the size of the keyspace that consists of passwords of this form? 12846 What is the equivalent key length in bits? 42 Assuming that you could check one password every 10-10 seconds, what is the worst case running time for cracking this password by brute force search (in days)? Now assume that the user used only 28 characters from the keyboard. What is the key length in bits in this case? How many days, in the worst case, would it take to break this weaker password? You can't round to the nearest day here be as exact as possible. Supposing you used only 28 characters, how long is the shortest password that achieves 177 bits of security