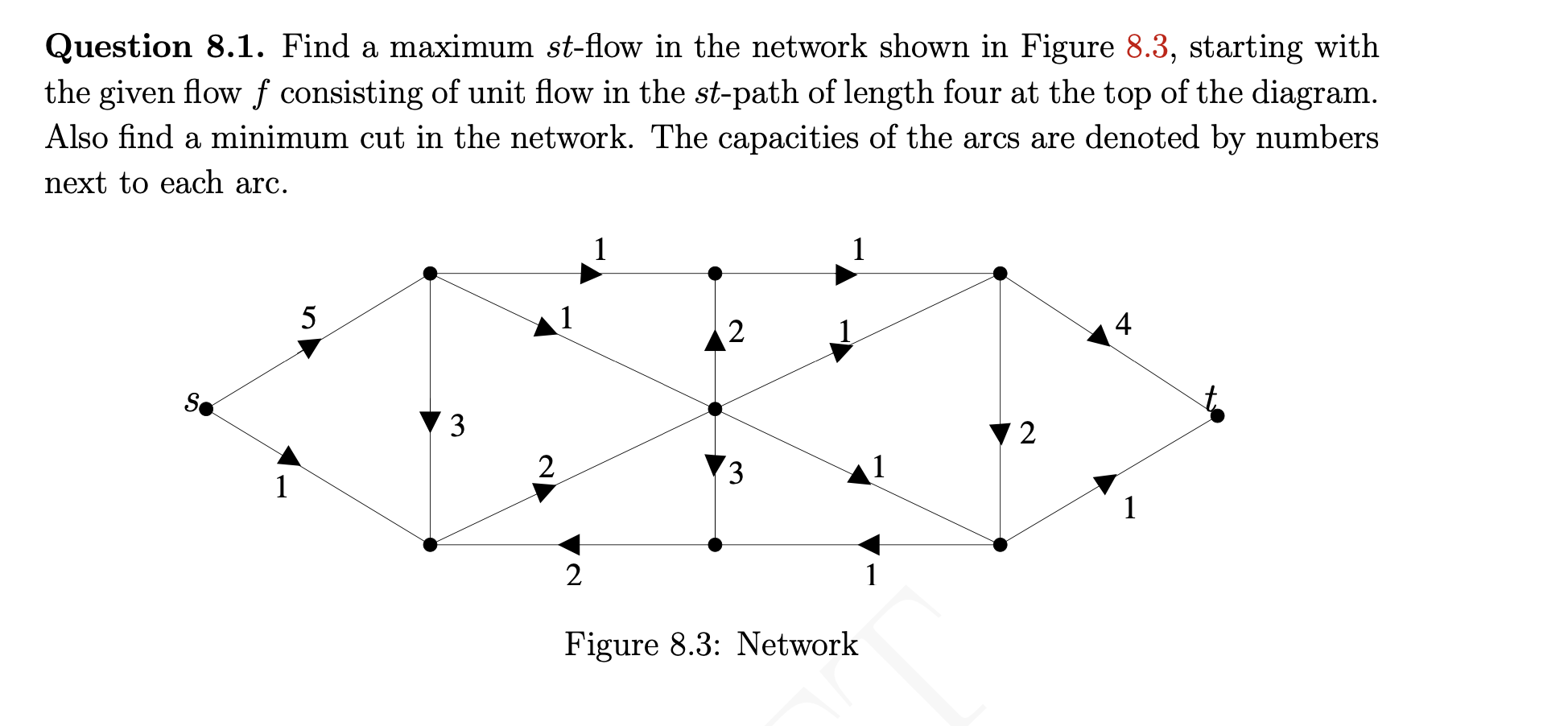
Question: PLEASE ANSWER USING THE THEOREM ABOVE DON'T COPY SOMEONE ELSE'S ANSWER AND PROVIDED CLEAR EXPLAINATIONS. Question 8.1. Find a maximum st-flow in the network shown

PLEASE ANSWER USING THE THEOREM ABOVE DON'T COPY SOMEONE ELSE'S ANSWER AND PROVIDED CLEAR EXPLAINATIONS.
Question 8.1. Find a maximum st-flow in the network shown in Figure 8.3, starting with the given flow f consisting of unit flow in the st-path of length four at the top of the diagram. Also find a minimum cut in the network. The capacities of the arcs are denoted by numbers next to each arc. Figure 8.3: Network As we stated, the proof of the Max-Flow Min-Cut Theorem gives an algorithm for finding a maximum flow as well as a minimum cut. To construct a maximum flow f and a minimum cut (S,S), proceed as follows: start by letting f be the zero flow and S={s} where s is the source. Construct a set S as in the theorem: whenever there is an arc (x,y) such that f(x,y)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


