Please check what should i add to the code to complete this question (it is python). Thank you very much

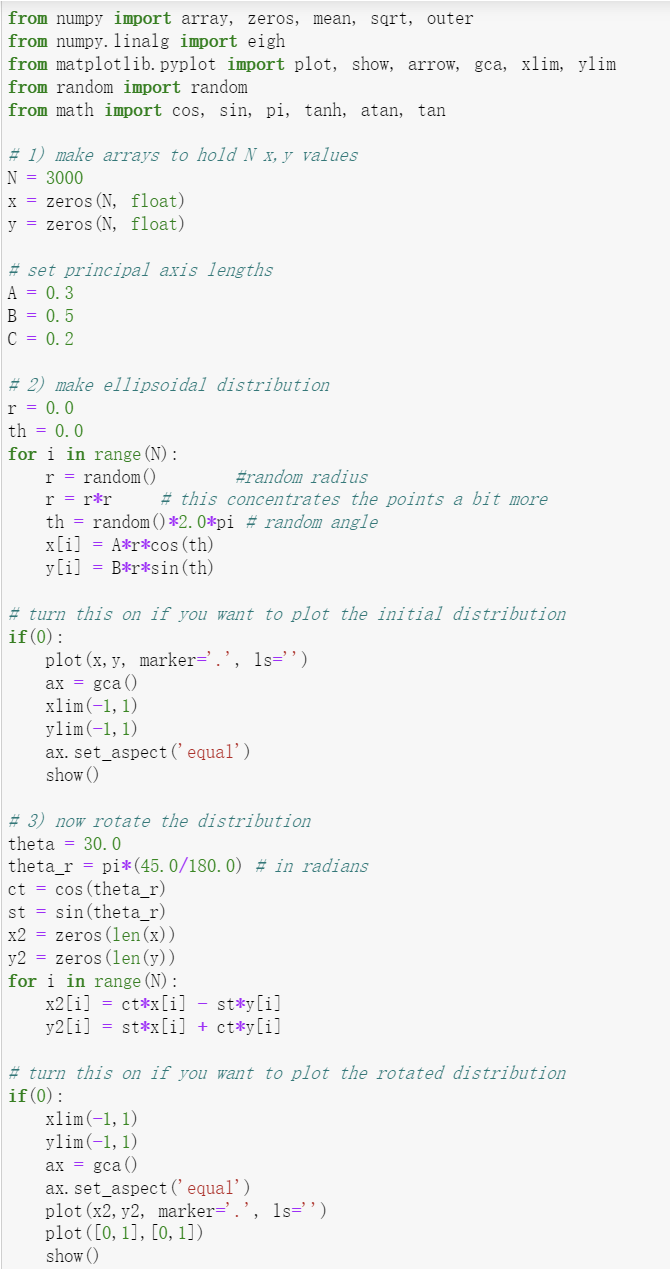
Suppose we represent an extended 2D system as a set of N equal mass elements or particles, with positions (xi,yi). The moment of inertia tensor is a matrix I such that the angular momentum vector of the system is L=I, where is the angular velocity vector. The coefficients of I are: I00=(yiy)2I01=(xix)(yiy)I10=(yiy)(xix)I11=(xix)2 where x=(1/N)xi and y=(1/N)yi are the average values of these coordinates. Then the eigenvectors of the moment of inertia tensor are the principal axes, or symmetry axes, of the system. a) Using the code below, you can generate a rotated, ellipsoidal distribution of points in 2D. Calculate the mean values of the xi and yi, and then the moment of inertia tensor. b) Determine the eigenvectors of the moment of inertia tensor (print them out), and plot these as arrows starting from x,y, along with the rotated points, show they are indeed the axes of symmetry. Hint: note that moment of inertia tensors are real and symmetric, and thus hermitian; this may affect the Python function(s) you choose to use. Suppose we represent an extended 2D system as a set of N equal mass elements or particles, with positions (xi,yi). The moment of inertia tensor is a matrix I such that the angular momentum vector of the system is L=I, where is the angular velocity vector. The coefficients of I are: I00=(yiy)2I01=(xix)(yiy)I10=(yiy)(xix)I11=(xix)2 where x=(1/N)xi and y=(1/N)yi are the average values of these coordinates. Then the eigenvectors of the moment of inertia tensor are the principal axes, or symmetry axes, of the system. a) Using the code below, you can generate a rotated, ellipsoidal distribution of points in 2D. Calculate the mean values of the xi and yi, and then the moment of inertia tensor. b) Determine the eigenvectors of the moment of inertia tensor (print them out), and plot these as arrows starting from x,y, along with the rotated points, show they are indeed the axes of symmetry. Hint: note that moment of inertia tensors are real and symmetric, and thus hermitian; this may affect the Python function(s) you choose to use