PLEASE CHOOSE THE CORRECT ANSWER AND PUT THE ANSWER CLEAR AS POSSIBLE, THANK YOU.

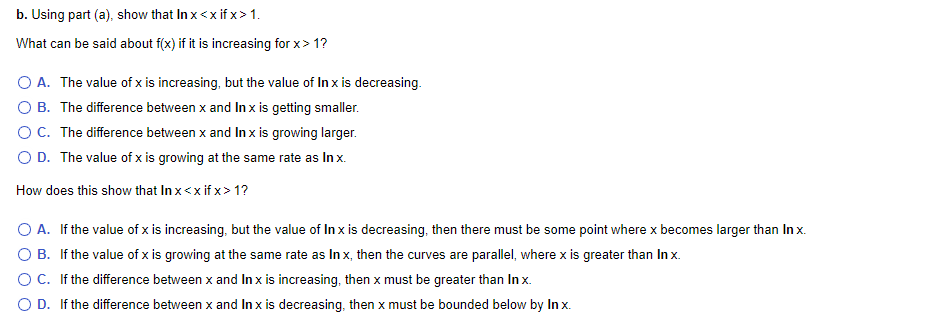
Complete parts a. and b. below. a. Prove that f(x) = x - In x is increasing for x > 1. First, find the derivative. f' (x ) = What property of the derivative can be used to show the function is increasing? O A. The derivative is decreasing for x > 1. O B. The derivative is positive for x > 1. O C. The derivative approaches to one as x approaches infinity. O D. The derivative is undefined at x = 0.b. Using part (a), show that In x 1. What can be said about f(x) if it is increasing for x > 1? O A. The value of x is increasing, but the value of In x is decreasing. O B. The difference between x and In x is getting smaller. O C. The difference between x and In x is growing larger. O D. The value of x is growing at the same rate as In x. How does this show that In x 1? O A. If the value of x is increasing, but the value of In x is decreasing, then there must be some point where x becomes larger than In x. O B. If the value of x is growing at the same rate as In x, then the curves are parallel, where x is greater than In x. O C. If the difference between x and In x is increasing, then x must be greater than In x. O D. If the difference between x and In x is decreasing, then x must be bounded below by In x