Please code this in OCaml language. You only need to code the uniq function that is described below using ONLY map, fold, and/or fold_right functions provided in the funs.ml and funs.mli files below.

For this code, please DO NOT use recursion nor recursive helpers, and DO NOT use any List Library methods as shown here: https://v2.ocaml.org/api/List.html

So no List.iter or List.rev or anything that uses List Library methods. The order of the output list doesn't matter for uniq, so things like List.sort and List.rev shouldn't be needed anyway.

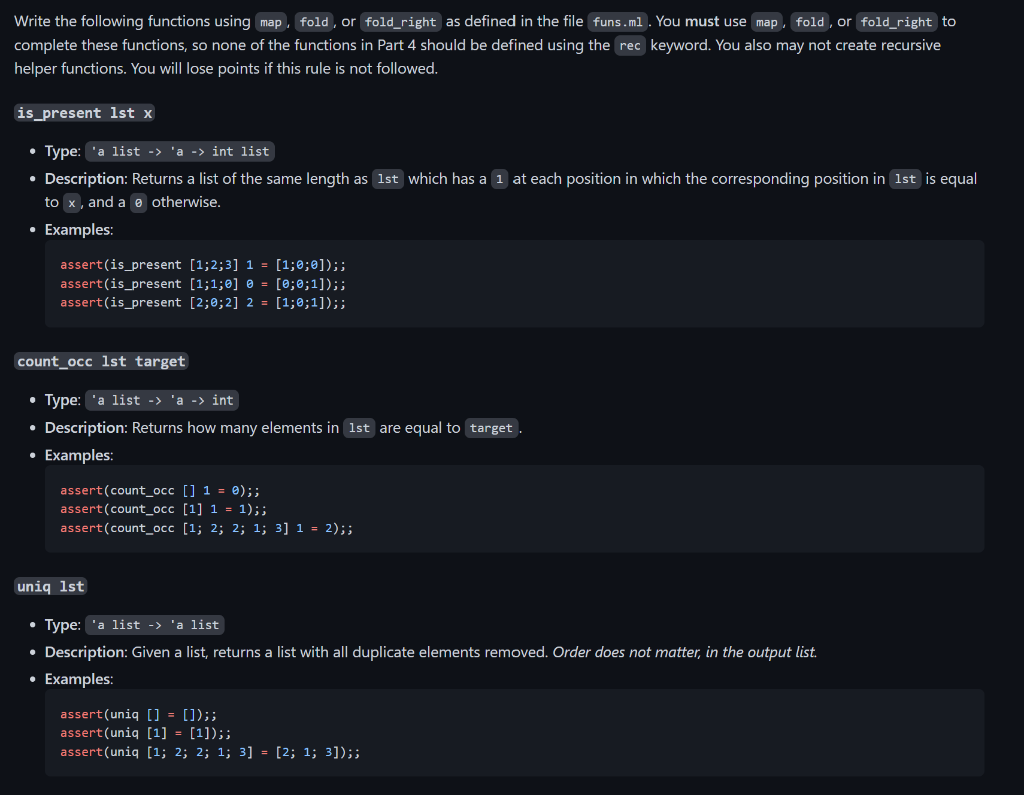
funs.ml code for: map, fold, and fold_right. I have also provided the types for funs.ml functions

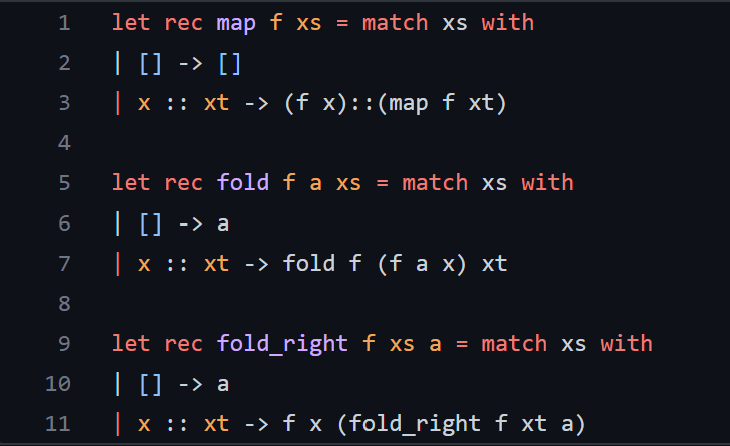
I have also coded the other two functions, which should be the only helper functions that can be used for uniq

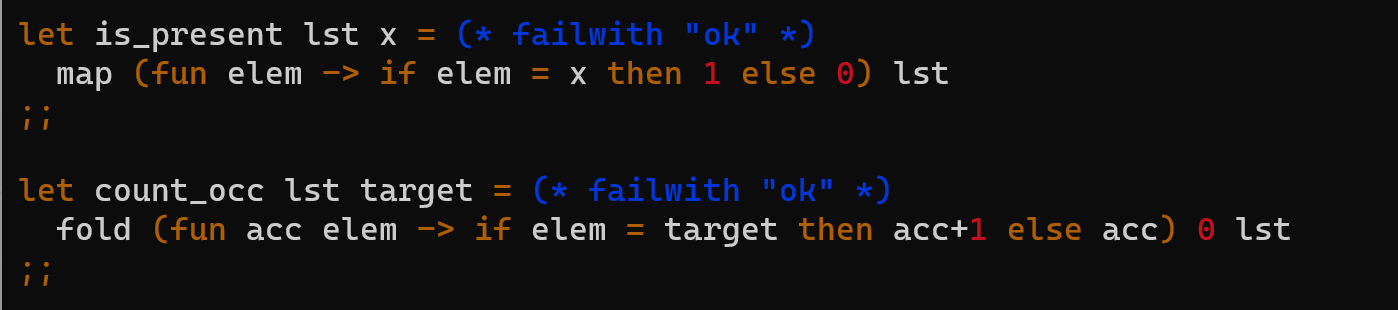
Again, please do not use recursion nor recursive helper for this code, and do not use list library methods. This uniq function should be doable with just map, fold, and fold_right, along with the two helper functions is_present and count_occ

Please make sure the code for uniq actually works as intended, and please show with proof (you can use the examples to show if the uniq is working), and know that is_present returns a list of 1 and 0s, and that count_occ returns an integer of how many times the target is within the list.

Write the following functions using map, fold, or fold_right as defined in the file funs.m1. You must use map, fold, or fold_right to complete these functions, so none of the functions in Part 4 should be defined using the rec keyword. You also may not create recursive helper functions. You will lose points if this rule is not followed. is_present lst x - Type: 'a list ' a int list - Description: Returns a list of the same length as 1 st which has a 1 at each position in which the corresponding position in 1 st is equal to x, and a otherwise. - Examples: \( \begin{aligned} \text { assert(is_present }[1 ; 2 ; 3] 1 & =[1 ; \theta ; \theta]) ; \\ \text { assert(is_present }[1 ; 1 ; \theta] \theta & =[0 ; \theta ; 1]) ; \\ \text { assert(is_present }[2 ; 0 ; 2] 2 & =[1 ; 0 ; 1]) ;\end{aligned} \) count_occ lst target - Type: 'a list ' a int - Description: Returns how many elements in lst are equal to target. - Examples: assert (count_occ [] 1=0);; assert ( count_occ [1]1=1);; assert(count_occ [1;2;2;1;3]1=2);; uniq lst - Type: 'a list 'a list - Description: Given a list, returns a list with all duplicate elements removed. Order does not matter, in the output list. - Examples: assert( uniq []=[]);; assert( uniq [1]=[1]);; assert( uniq [1;2;2;1;3]=[2;1;3]);; let is_present lst x=( failwith "ok" *) map (fun elem if elem =x then 1 else 0 ) lst i; let count_occ lst target =( failwith "ok" ) fold (fun acc elem if elem = target then acc+ 1 else acc) 0 lst