Question: Please complete the attached file. Write a function for the False position. Write your conclusions Document each line of the code Bracketing The bracketing is
Please complete the attached file.
Write a function for the False position.
Write your conclusions
Document each line of the code
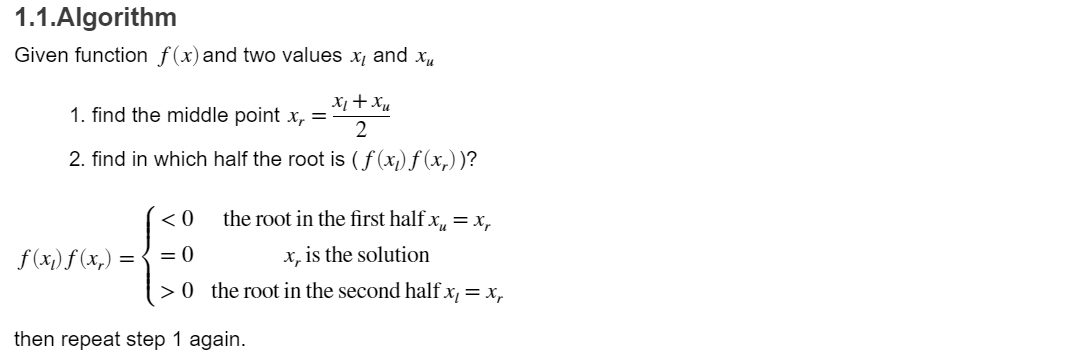


![and x, in half [blah blah] f(m) 1 2 50 100 150](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66fa3e91e32f9_04966fa3e916305d.jpg)

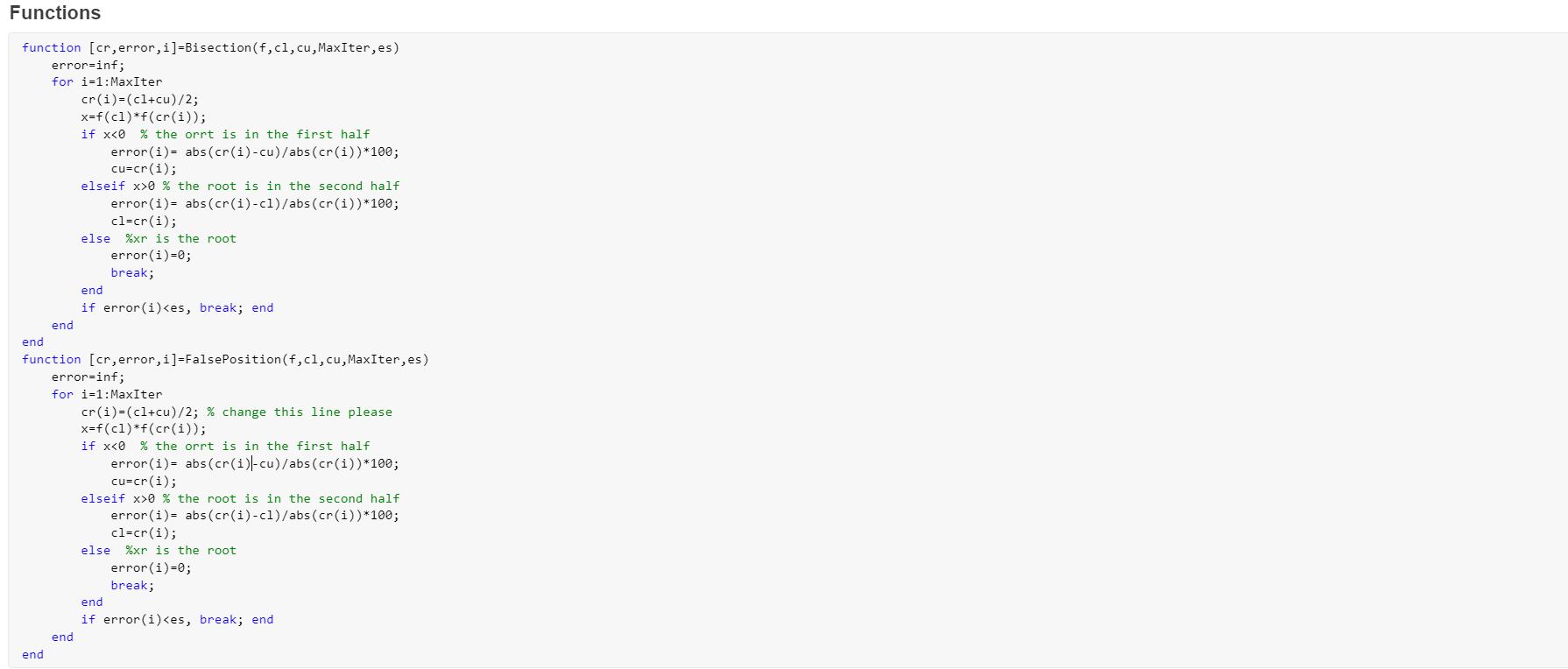
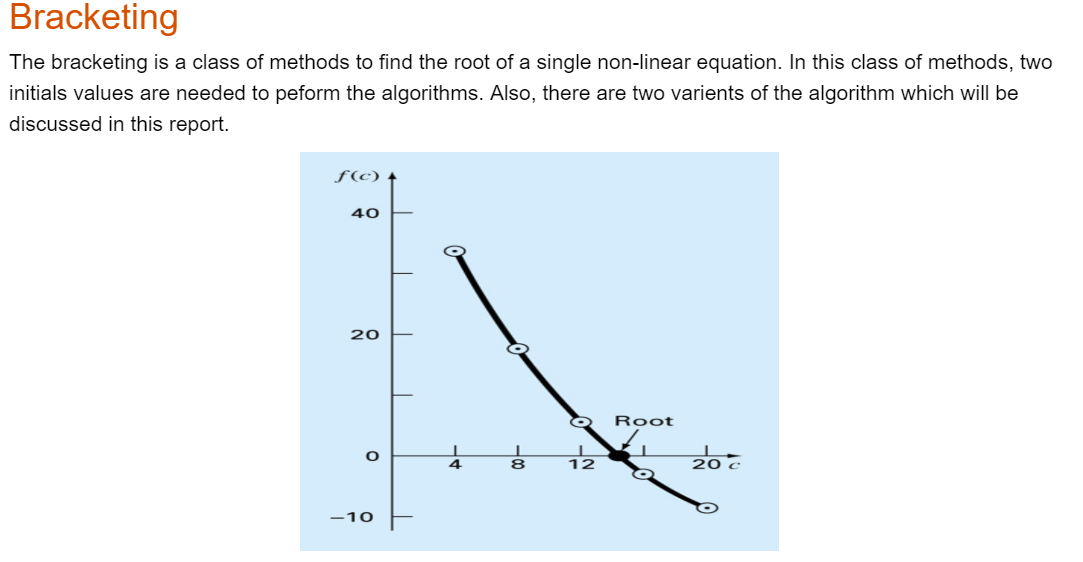
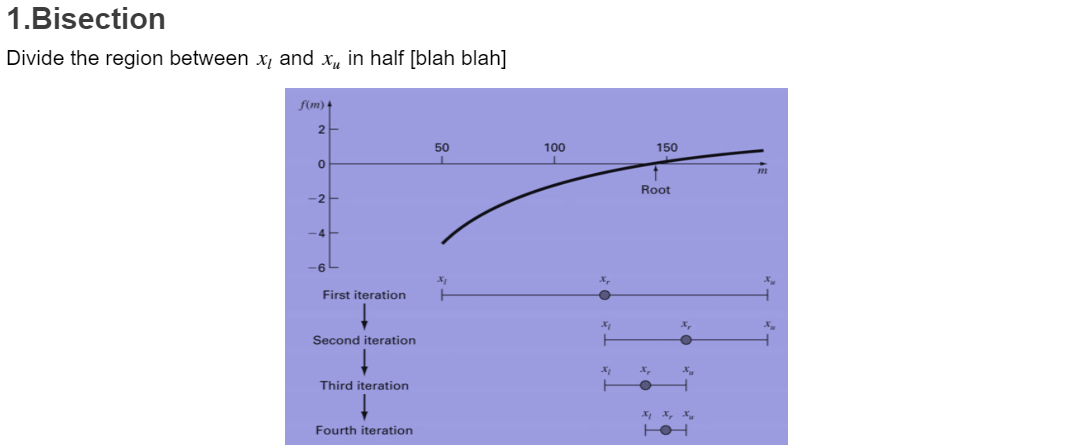
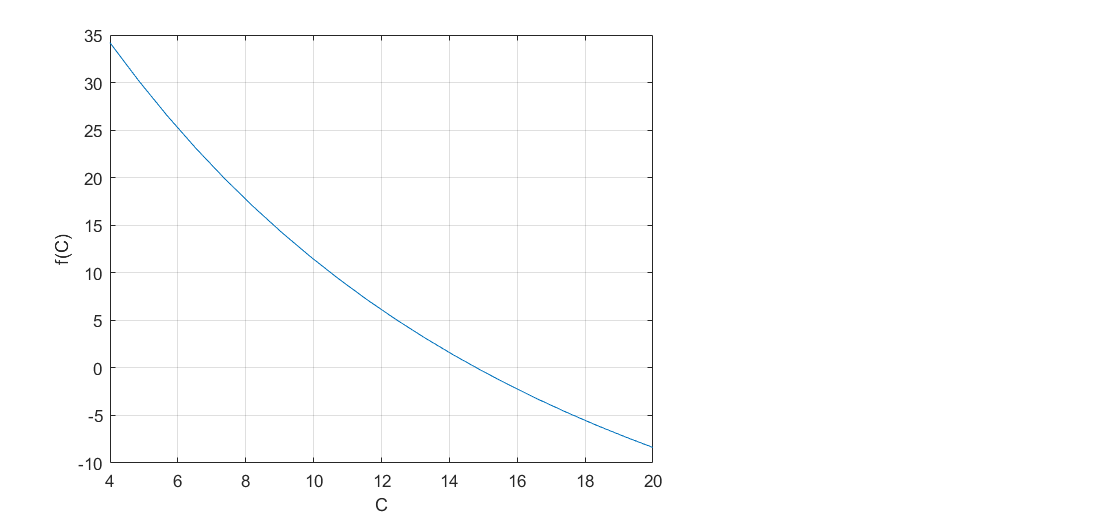
Bracketing The bracketing is a class of methods to find the root of a single non-linear equation. In this class of methods, two initials values are needed to peform the algorithms. Also, there are two varients of the algorithm which will be discussed in this report. f(c) 40 20 Root o 1 4 8 12 20 -10 1.Bisection Divide the region between x, and x, in half [blah blah] f(m) 1 2 50 100 150 0 m 1 Root -2 -4 -6 First iteration . Second iteration HH . Third iteration Fourth iteration 1.1.Algorithm Given function f(x) and two values x, and xu x1 + xu 1. find the middle point x, = 2 2. find in which half the root is (f(x) f (x,))? f (x1) f(x,) = 0 the root in the second half x, = x, then repeat step 1 again. 1.2.Code and Results f=@(c) 9.81./c*68.1. *(1-exp(-c./68.1.*10) )-40; %the function to find the root for c=linspace(4,20,20); plot(c, f(c)); xlabel('C') ylabel('f(C)') grid on; 35 30 25 20 15 f(C) 10 5 0 -5 -10 4 6 8 10 12 14 16 18 20 This plot allow us to find the values of x1 = 14 and xu = 16 cl=14; cu=16; Maxiter=100; es=0.0001; [cr, error, i]=Bisection(f,cl,cu,MaxIter,es); plot(log10(error)) 0 - 1 -2 -3 -4 -5 0 2 4 6. 8 10 12 14 16 18 i i = 18 error error = 1x18 6.6667 3.4483 1.6949 0.8403 0.4219 0.2114 0.1056 0.0528 0.0264 0.0132 0.0066 2.False Position 2.1.Algorithm 2.2.Code and Results Conclusion [comparison between Bisection and false position] Functions function (cr, error, i]=Bisection(f,cl,cu, MaxIter, es) error=inf; for i=1: MaxIter cr(i)=(cl+cu)/2; x=f(cl) f(cr(i)); if x0 % the root is in the second half error(i)= abs(cr(i)-cl)/abs(cr(i))*100; cl=cr(i); else %xr is the root error(i)=0; break; end if error(i)
Step by Step Solution
There are 3 Steps involved in it
To write the False Position method function we can follow these steps False Position Algorithm The F... View full answer

Get step-by-step solutions from verified subject matter experts


