please do clear steps

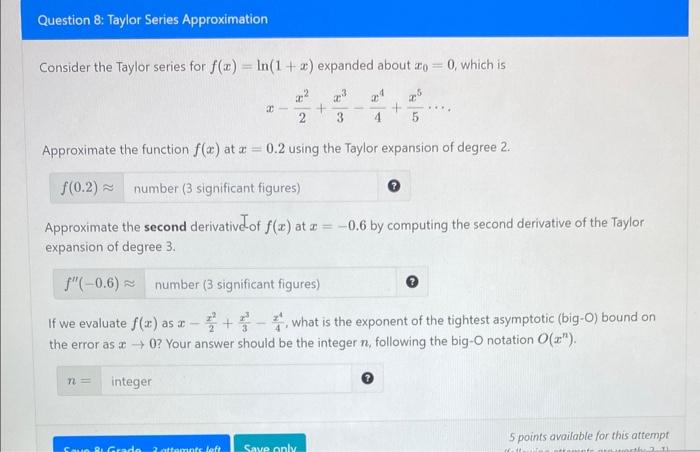
Consider the Taylor series for f(x)=ln(1+x) expanded about x0=0, which is x2x2+3x34x4+5x5. Approximate the function f(x) at x=0.2 using the Taylor expansion of degree 2 . f(0.2) Approximate the second derivative-of f(x) at x=0.6 by computing the second derivative of the Taylor expansion of degree 3. f(0.6)= If we evaluate f(x) as x2x2+3x34x4, what is the exponent of the tightest asymptotic (big-0) bound on the error as x0 ? Your answer should be the integer n, following the big-O notation O(xn)