Please do its Part 3 for me

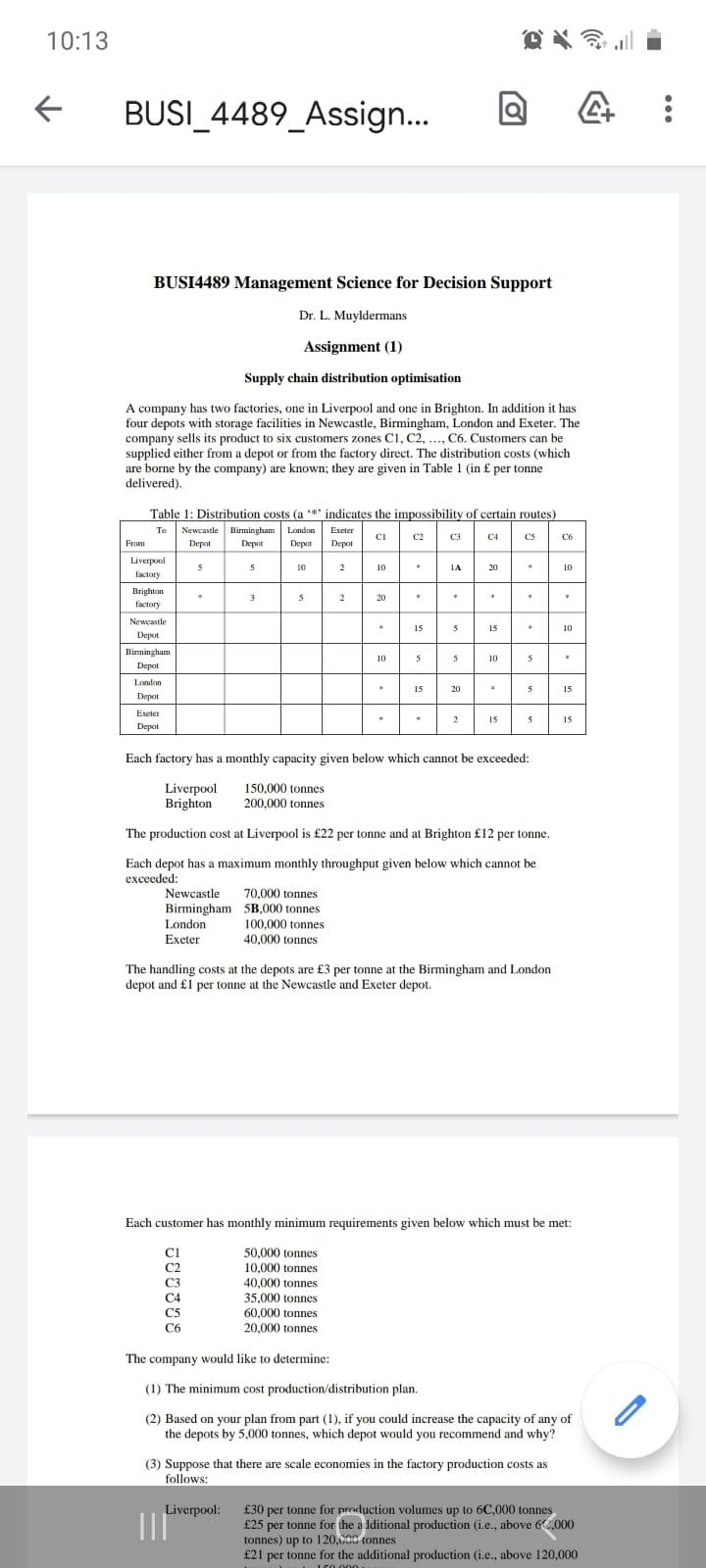
10:13 BUSI_4489_Assign... : BUSI4489 Management Science for Decision Support Dr. L. Muyldermans Assignment (1) Supply chain distribution optimisation A company has two factories, one in Liverpool and one in Brighton. In addition it has four depots with storage facilities in Newcastle, Birmingham, London and Exeter. The company sells its product to six customers zones CI, C2, ..., C6. Customers can be supplied either from a depot or from the factory direct. The distribution costs (which are borne by the company) are known; they are given in Table 1 (in per tonne delivered). Exeter C6 IA . 10 Table 1: Distribution costs (a *** indicates the impossibility of certain routes) Newcastle Birmingham Eliminyum London CI 3 From Depot Depot C4 Depit Depot Liverpool 5 5 10 2 10 20 factory Brighton S 2 20 factory Newcastle 15 5 15 . Depot Birmingham 10 5 5 10 5 Depot London 15 20 5 Depot Exeter 2 2 15 5 Depot . 10 15 15 Each factory has a monthly capacity given below which cannot be exceeded: Liverpool Brighton 150,000 tonnes 200,000 tonnes The production cost at Liverpool is 22 per lonne and at Brighton 12 per tonne. Each depot has a maximum monthly throughput given below which cannot be exceeded: Newcastle 70,000 tonnes Birmingham 58,000 tonnes London 100.000 tonnes Exeter 40.000 tonnes The handling costs at the depots are 3 per tonne at the Birmingham and London depot and l per tonne at the Newcastle and Exeter depot. Each customer has monthly minimum requirements given below which must be met: ci C2 C3 C4 CS C6 50.000 tonnes 10,000 tonnes 40.000 tonnes 35,000 tonnes 60,000 tonnes 20,000 tonnes The company would like to determine: (1) The minimum cost production/distribution plan. (2) Based on your plan from part (1), if you could increase the capacity of any of the depots by 5.000 tonnes, which depot would you recommend and why? (3) Suppose that there are scale economies in the factory production costs as follows: Liverpool: 30 per tonne for production volumes up to 6C.000 tonnes 25 per tonne for the a Iditional production (i.e., above 60,000 tonnes) up to 120.000 tonnes 21 per tonne for the additional production (.e., above 120,000 Each customer has monthly minimum requirements given below which must be met: CI C2 C3 C4 CS C6 50.000 tonnes 10,000 tonnes 40.000 tonnes 35.000 tonnes 60.000 tonnes 20.000 tonnes The company would like to determine: (1) The minimum cost production distribution plan. (2) Based on your plan from part (1), if you could increase the capacity of any of the depots by 5,000 tonnes, which depot would you recommend and why? (3) Suppose that there are scale economies in the factory production costs as follows: Liverpool 30 per tonne for production volumes up to 6C,000 tonnes 25 per tonne for the additional production (i.e., above 60.000 tonnes) up to 120,000 tonnes 21 per tonne for the additional production (i.e., above 120,000 tonnes) up to 150,000 tonnes Brighton: 15 per tonne for production volumes up to 100.000 tonnes 12 per tonne for the additional production (i.c., above 100,000 tonnes) up to 160,000 tonnes 10 per tonne for the additional production (i.e., above 160,000 tonnes) up to 200,000 tonnes What is the new minimum cost production/distribution plan? Report structure: For part (1): Formulate this distribution problem as a linear programme, enter the model into Excel and obtain its solution using Solver. Your answer to part (1) must contain: (1) the LP formulation with a clear explanation of the decision variables, the objective function and the constraints. You must explain the constraints briefly (2) A screenshot of the model's setup in Excel. Note that the structure of the LP formulation (that is all variables, constraints and coefficients) must be clearly visible in Excel (3) A brief discussion of the optimal production/distribution plan. Graphs and/or diagrams may be helpful to structure the problem and/or to discuss results. Solver answer and sensitivity report() should come in Appendix to your report. 3/3 For part (2): Explain your approach and reasoning (how did you derive your result) and also show the impact of this modification on the optimal solution from part (1). For part (3): Explain your approach and specifically, how you introduced the piecewise linear production costs in the model and how you adapted the setup in Excel. Solve the new model and briefly discuss its solution. Notes: the values for A, B and Care on your personal student ID. A is the third digit on your ID, B is the fourth digit and C is the last digit on your ID. For example, If your ID is 3451230, then A = 5 and B = 1, and C=0, so that the transportation cost for supplying customer C3 from the Liverpool factory is 15 per tonne; the capacity of the Birmingham depot is 51,000 tonnes, and the first production cost breakpoint at the Liverpool factory is for a production volume of 60,000 tonnes. Please submit your report before the due date (19th November, 3pm) electronically through Moodle. This is an individual assignment: you have to write up your report individually. References are not required for this coursework. Good luck! 10:13 BUSI_4489_Assign... : BUSI4489 Management Science for Decision Support Dr. L. Muyldermans Assignment (1) Supply chain distribution optimisation A company has two factories, one in Liverpool and one in Brighton. In addition it has four depots with storage facilities in Newcastle, Birmingham, London and Exeter. The company sells its product to six customers zones CI, C2, ..., C6. Customers can be supplied either from a depot or from the factory direct. The distribution costs (which are borne by the company) are known; they are given in Table 1 (in per tonne delivered). Exeter C6 IA . 10 Table 1: Distribution costs (a *** indicates the impossibility of certain routes) Newcastle Birmingham Eliminyum London CI 3 From Depot Depot C4 Depit Depot Liverpool 5 5 10 2 10 20 factory Brighton S 2 20 factory Newcastle 15 5 15 . Depot Birmingham 10 5 5 10 5 Depot London 15 20 5 Depot Exeter 2 2 15 5 Depot . 10 15 15 Each factory has a monthly capacity given below which cannot be exceeded: Liverpool Brighton 150,000 tonnes 200,000 tonnes The production cost at Liverpool is 22 per lonne and at Brighton 12 per tonne. Each depot has a maximum monthly throughput given below which cannot be exceeded: Newcastle 70,000 tonnes Birmingham 58,000 tonnes London 100.000 tonnes Exeter 40.000 tonnes The handling costs at the depots are 3 per tonne at the Birmingham and London depot and l per tonne at the Newcastle and Exeter depot. Each customer has monthly minimum requirements given below which must be met: ci C2 C3 C4 CS C6 50.000 tonnes 10,000 tonnes 40.000 tonnes 35,000 tonnes 60,000 tonnes 20,000 tonnes The company would like to determine: (1) The minimum cost production/distribution plan. (2) Based on your plan from part (1), if you could increase the capacity of any of the depots by 5.000 tonnes, which depot would you recommend and why? (3) Suppose that there are scale economies in the factory production costs as follows: Liverpool: 30 per tonne for production volumes up to 6C.000 tonnes 25 per tonne for the a Iditional production (i.e., above 60,000 tonnes) up to 120.000 tonnes 21 per tonne for the additional production (.e., above 120,000 Each customer has monthly minimum requirements given below which must be met: CI C2 C3 C4 CS C6 50.000 tonnes 10,000 tonnes 40.000 tonnes 35.000 tonnes 60.000 tonnes 20.000 tonnes The company would like to determine: (1) The minimum cost production distribution plan. (2) Based on your plan from part (1), if you could increase the capacity of any of the depots by 5,000 tonnes, which depot would you recommend and why? (3) Suppose that there are scale economies in the factory production costs as follows: Liverpool 30 per tonne for production volumes up to 6C,000 tonnes 25 per tonne for the additional production (i.e., above 60.000 tonnes) up to 120,000 tonnes 21 per tonne for the additional production (i.e., above 120,000 tonnes) up to 150,000 tonnes Brighton: 15 per tonne for production volumes up to 100.000 tonnes 12 per tonne for the additional production (i.c., above 100,000 tonnes) up to 160,000 tonnes 10 per tonne for the additional production (i.e., above 160,000 tonnes) up to 200,000 tonnes What is the new minimum cost production/distribution plan? Report structure: For part (1): Formulate this distribution problem as a linear programme, enter the model into Excel and obtain its solution using Solver. Your answer to part (1) must contain: (1) the LP formulation with a clear explanation of the decision variables, the objective function and the constraints. You must explain the constraints briefly (2) A screenshot of the model's setup in Excel. Note that the structure of the LP formulation (that is all variables, constraints and coefficients) must be clearly visible in Excel (3) A brief discussion of the optimal production/distribution plan. Graphs and/or diagrams may be helpful to structure the problem and/or to discuss results. Solver answer and sensitivity report() should come in Appendix to your report. 3/3 For part (2): Explain your approach and reasoning (how did you derive your result) and also show the impact of this modification on the optimal solution from part (1). For part (3): Explain your approach and specifically, how you introduced the piecewise linear production costs in the model and how you adapted the setup in Excel. Solve the new model and briefly discuss its solution. Notes: the values for A, B and Care on your personal student ID. A is the third digit on your ID, B is the fourth digit and C is the last digit on your ID. For example, If your ID is 3451230, then A = 5 and B = 1, and C=0, so that the transportation cost for supplying customer C3 from the Liverpool factory is 15 per tonne; the capacity of the Birmingham depot is 51,000 tonnes, and the first production cost breakpoint at the Liverpool factory is for a production volume of 60,000 tonnes. Please submit your report before the due date (19th November, 3pm) electronically through Moodle. This is an individual assignment: you have to write up your report individually. References are not required for this coursework. Good luck