Please do the following problem in excel, and show the formuals when showing work.

Suppose that there are many stocks in the security market and that the characteristics of stocks A and B are given as follows:

Suppose that it is possible to borrow at the risk-free rate, rf. What must be the value of the risk-free rate? (Hint: Think about constructing a risk-free portfolio from stocks A and B.) (Do not round intermediate calculations. Round your answer to 3 decimal places.)

please show the excel formulas used in excel *

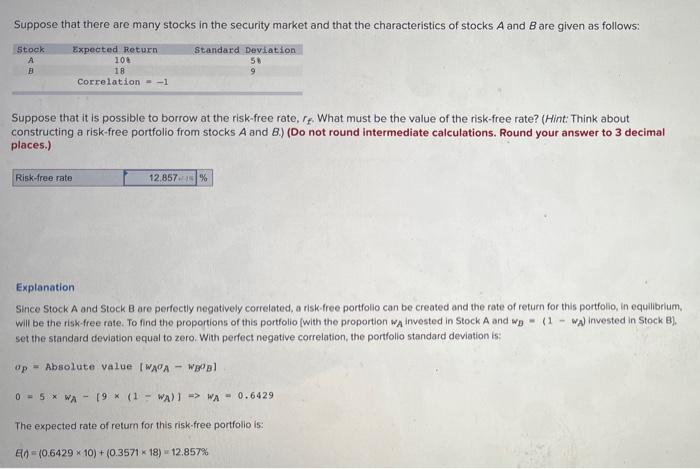
Suppose that there are many stocks in the security market and that the characteristics of stocks A and B are given as follows: Stock B Expected Return 100 18 Correlation-1 Standard Deviation 58 9 Suppose that it is possible to borrow at the risk-free rate, rr. What must be the value of the risk-free rate? (Hint: Think about constructing a risk-free portfolio from stocks A and B.) (Do not round Intermediate calculations. Round your answer to 3 decimal places.) Risk-free rate 12.857% Explanation Since Stock A and Stock Bare perfectly negatively correlated, a risk free portfolio can be created and the rate of return for this portfolio, in equilibrium, will be the risk-free rate. To find the proportions of this portfolio (with the proportion wa invested in Stock A and we - (1 - wa) invested in Stock B), set the standard deviation equal to zero. With perfect negative correlation, the portfolio standard deviation is: Op = Absolute value IWAPA - W] 0 = 5* WA - 19 * (1 - WA) -> WA - 0.6429 The expected rate of return for this risk-free portfolio is: 60 - (0.6429 X 10) + (0.3571 18) 12.857%