Question: Please follow guidelines strictly, thank you Problem 2 (2.12.2) Show directly that any multiple of a Cauchy sequence is again a Cauchy sequence. Proof. Let
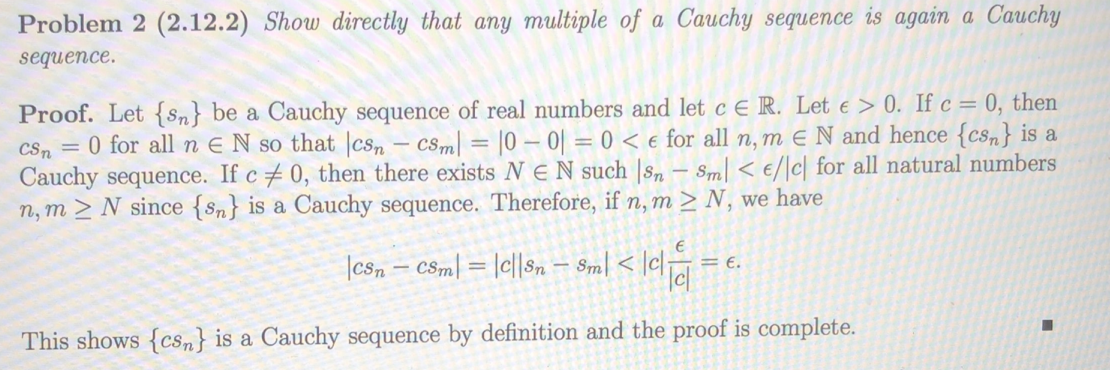

 Please follow guidelines strictly, thank you
Please follow guidelines strictly, thank you
Problem 2 (2.12.2) Show directly that any multiple of a Cauchy sequence is again a Cauchy sequence. Proof. Let {sn} be a Cauchy sequence of real numbers and let ce R. Let e > 0. If c = 0, then CSn = 0 for all n e N so that \csn csm= |0 - 0 = 0 N since {sn} is a Cauchy sequence. Therefore, if n, m > N, we have |csn csm/ = |el|sn sml
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


